11.Approximation
约 1408 个字 17 张图片 预计阅读时间 5 分钟
概述¶
对于NPC问题：
-
如果N的大小比较小，就算是\(O(2^N)\)的时间复杂度我们也可以接受
-
用多项式时间内的算法解决一部分重要的特殊的情况
-
或者放弃找最优解，而是找近似最优解的解。
Approximation Ratio（近似比）
定义：假设原问题解的值域是正数，最优解是\(C^*\)，近似算法得到的解是\(C\)，将两个相除（让比值大于1），如果这个比值能够被一个值bound住，那么我们就说算法有一个近似比\(\rho\)。
给出一个限制条件\(\epsilon\)，也就是需要给出的算法的近似比为\(1+ \epsilon\)，也就是说一个近似方案有两个参数，一个是问题的规模另一个是近似比限制条件\(\epsilon\)，在计算时间复杂度的时候我们需要进行权衡。
比如\(O(n^{2/ \epsilon })\)，随着\(\epsilon\)的减少，时间复杂度呈指数级上升；对于这类对于特定的\(\epsilon\)，时间复杂度在多项式时间的算法我们称为PTAS(polynomial-time approximation scheme)
而\(O((1/\epsilon)^2n^3)\)，这类算法和n和\(\epsilon\)都呈现多项式的关系，对于这类算法可以对近似比的要求更加严格。对于这类关于\(\epsilon\)和n都呈多项式时间复杂度的算法我们称为FPTAS(fully polynomial-time approximation scheme)
算法的三个方面¶
我们这一节课学的都是B+C的算法
Bin Packing¶
给定N个items，每个item的size是\(S_1, S_2, ..., S_N\)，\(0 < S_i \le 1\)。找出最少数量的bin来容纳所有的item，这是一个npc问题。
On-line Algorithms¶
Next Fit¶
当我们读到一个item，看能否放进当前的bin，如果不能就开一个新的bin。这个算法只需要扫描一遍，时间复杂度为\(O(N)\)。
theorem
Let M be the optimal number of bins required to pack a list I of items. Then next fit never uses more than 2M – 1 bins. There exist sequences such that next fit uses 2M – 1 bins.
proof
First Fit¶
当我们读到一个item，看能否放进之前的所有bin，如果不能就开一个新的bin。这个算法每次都要扫描之前的所有bin，所以时间复杂度为\(O(NlogN)\)。
theorem
Let M be the optimal number of bins required to pack a list I of items. Then first fit never uses more than 17M / 10 bins. There exist sequences such that first fit uses 17(M – 1) / 10 bins.
Best Fit¶
当我们读到一个item，看能否放进之前的所有bin，找出剩余空间最小的bin放进去，如果不能就开一个新的bin。这个算法和之前的Fisrt Fit是一样的1.7。
例子¶
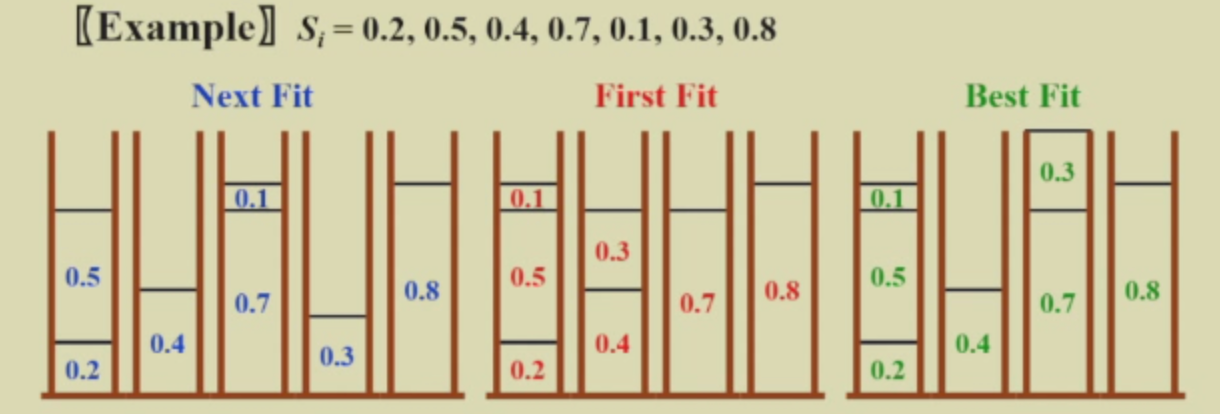
但是这些算法都是on-line，就是当前做了decision之后，就不能改变了。
theorem
对于on-line的算法，There are inputs that force any on-line bin-packing algorithm to use at least 5/3 the optimal number of bins.
Off-line Algorithms¶
扫描所有的item之后才得出答案。先把item的大小进行排序，先放大的item，再放小的item。
Knapsack Problem¶
Fractional version¶
背包的容积给定为M，有N个物品，物品有代价 \(w_i\)和利益\(p_i\)，允许把物品按比例切分放入，求利益最大的装法。
from Carton手写笔记
0-1 version（NP-hard）¶
物品不能按照比例放入，要么放入要么不放入。
如果使用最大性价比的贪婪算法，比如\((w_1,w_2,w_3,w_4) = (1, 0.05, 0.05, 0.05)\)，\((p_1, p_2,p_3,p_4) = (10, 1, 1, 1)\)，最大性价比选的话会选择后面三个，不是最优解。
如果直接按照价值排序，不考虑性价比，价值高的物品能放进去就放进去，放不进去在考虑下一个，这样也可构造反例，不是最优解。
我们可以综合上述两种算法，取两种算法的最优解。
可以算出这种算法的近似比为2。
证明近似比为2
\(P_{max}\)：能放进来的物品中价值最大的那个； \(P_{opt}\)：0-1情况下的最大收益； \(P_{frac}\)：可切割版本下的最大收益； 易得\(P_{max} \le P_{opt} \le P_{frac}\)
\(P_{greedy}\)：0-1问题中用收益率贪婪算法得到的最大收益 \(P_{max} \le P_{greedy}\)，很好理解，因为算法是性价比贪婪和价值贪婪的两个取最大。
\(P_{opt} \le P_{frac} \le P_{max} +P_{greedy}\)，这个也很容易理解，greedy算法最后可能会有剩余，在这个时候把价值最大的物品塞进去，那么肯定比最优解的价值还高。
\(\Longrightarrow P_{opt}/P_{greedy} \le 1 + P_{max}/P_{greedy} \le 2\)
动态规划算法解决问题
设\(W_{i,p}\)是考虑完第i个物品之后利益为p时的最轻质量。
如果\(p_i > p\)，说明\(W_{i,p}\)并没有把第i个物品放进来，所以\(W_{i,p} = W_{i-1,p}\)；否则选择放入或者不放入总重量比较小的那个。
因为有i和p两个维度，而\(i = 1, ...,n\)，\(p = 1,...,nP_{max}\)，想乘即可，但是这个时间复杂度是伪多项式时间复杂度，因为\(P_{max}\)可以是n的指数级。比如十个物体，价值十个亿，动态规划的复杂度一下子就上去了。
动态规划代码到时候记忆一下！
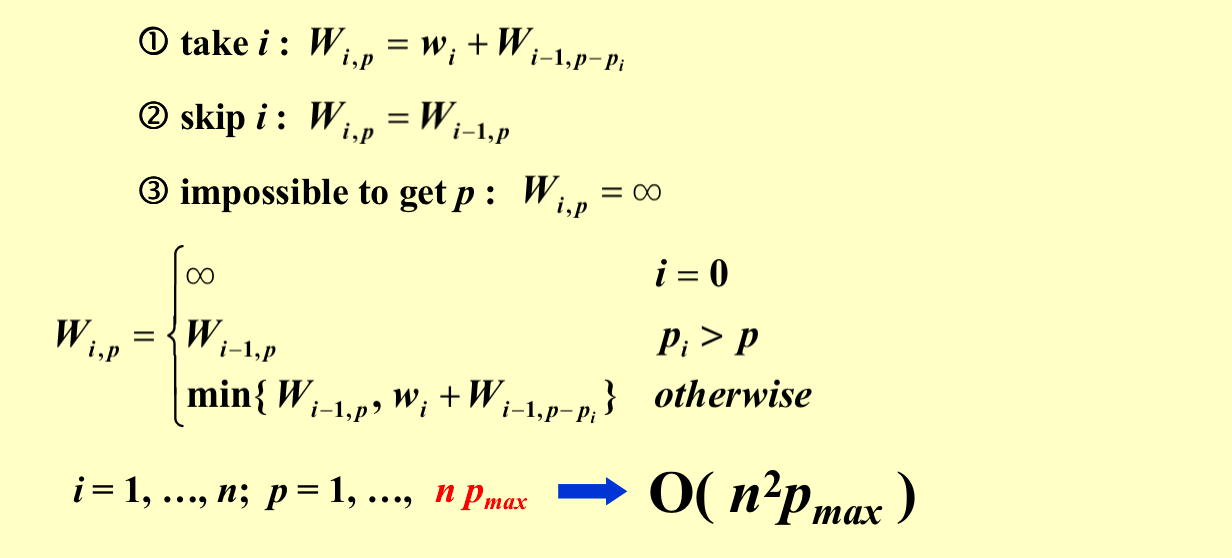
当\(p_{max}\)很大时，我们可以同时除以一个数（round方法）来使每个p都减少，这样可以节约时间，但是会有精度的损失。
from Carton手写笔记
K-center Problem¶
问题描述：平面上给定一堆集合，要求找出不超过K个圆心的位置，使得园覆盖所有点，而且radius（所有宿舍中离食堂最远的那个宿舍离食堂的距离尽可能短）最小。
思路：
找K个中心比较难，我们先找一个中心，但是这样就没有意义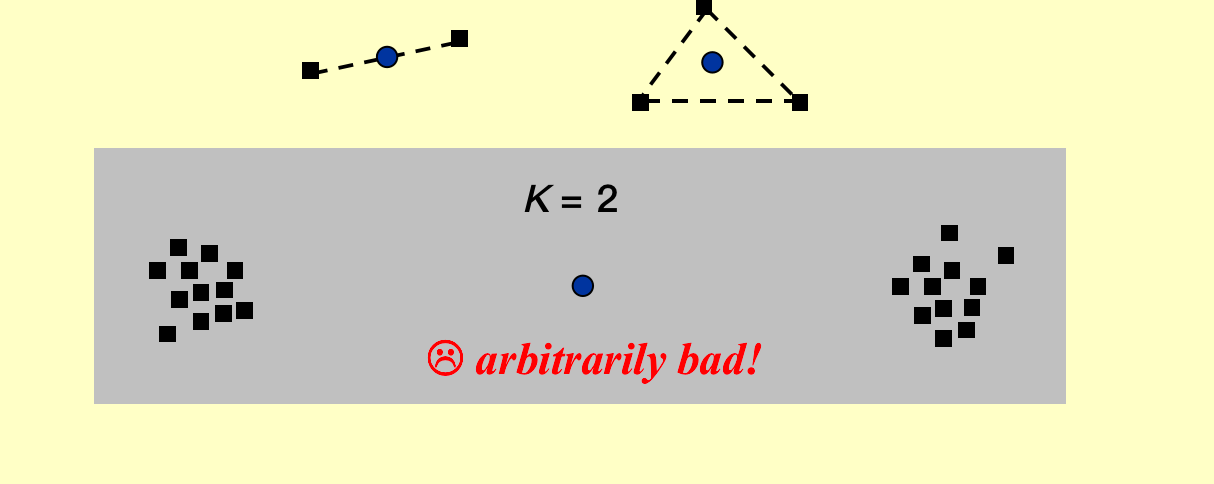
假设我们把食堂放到宿舍上，这样，假设原来的食堂放置最优解的长度为r，那么把食堂放在宿舍上还能覆盖到原来所有宿舍，长度最多为2r。
也就是说现在我们让食堂在宿舍上，这样他的最优解不会比原来的最优解的两倍差。
现在我们随机选一个点作为圆心，假设已经知道最优解是r，那么把和这个点相距2r以内的点全部删除，因为这些点肯定已经被覆盖了。再从剩下的点里面随机选一个点，如此重复，直到所有点点都被删除。如果这些被选中的中心点的数量\(\le K\)，那么结束。否则不存在解，也就是半径r是错的。
Theorem
如果这个算法选择的中心超过K个，那么原来的问题的最优解半径也肯定比r大。
proof：
假设我们近似算法选择了K+1个点作为中心，而原问题最优解只有K个中心，这时候肯定有2个中心被原问题的K个点包住，且距离\(\le r\)，根据三角形法则，这两个点的距离\(\le 2r\)，但是根据之前的算法描述这是不可能的，矛盾。
那么我们怎么确定r呢？我们可以直接使用二分法，一个一个r去试验，如果能找到就把r缩小，如果不能找到就把r放大。
因此我们得到了一个近似比为2的近似算法。
优化上述算法：
上述算法要二分来找r太繁琐，我们在找下一个中心的时候，不是随机选择\(\ge 2r\)的点，而是选择距离当前所有选中的中心最远的点（如果这个点都已经\(\le 2r\)，那说明你早就已经覆盖了所有点），把它加入中心的集合中，一共选择K次，直接输出就是答案。
Theorem
这个算法算出的最优解不差于原问题最优解的两倍。
proof：
假设最优解是r，那么一旦我们当前的算法返回\(>2r\)的解，那么至少有一个宿舍距离我们选出来的食堂是\(>2r\)的，并且被我们这个算法算出来的所有的距离都是\(>2r\)的。
现在我们用之前的随机算法再解一遍这个问题，外面二分出r带入这个算法，会发现至少有K+1个点他们之间的距离大于2r，那么和最优解为r冲突。
此类问题最好的近似比就是2，如果更小除非P=NP。
The End¶
参考资料
- ADSNotes_Algorithms.pdf(from Carton手写笔记)
- ADS11ppt
- 小角龙(18)复习笔记.pdf
- JerryG(20)复习笔记.pdf
- 智云课堂：2023yds
评论
本文总阅读量次