12.Local Search
约 1594 个字 10 行代码 18 张图片 预计阅读时间 5 分钟
1. 概述¶
做一个初始的猜测,然后在猜测的点周边,用更优解来替代猜测的点,不断迭代逼近最优解。所以局部搜索的想法就是从不准确的解作为开始,不断搜索该点周围更加接近最优的解来替代,如此重复来逼近最优解。逼近最优解不一定会在有限步骤内停止。
Local Search的结构

from Carton手写笔记

算法:
- 可行解作为一个起点;
- 在S的邻居中按照某一种规则去找到其中的一个更加接近最优解的邻居。
- 如果最好的邻居都比自己差,那么算法结束;否则,把当前点移动到邻居身上。
2. 顶点覆盖问题¶
问题概述:在无向图中找最小的点集,对于每一条边,至少有一个点在点集中。
构造算法:首先需要找到一个可行解,直接取所有的点为起始解。cost(S)定义为S中点的个数。S'是S的邻居,S'从S中去掉一个点得到。
案例: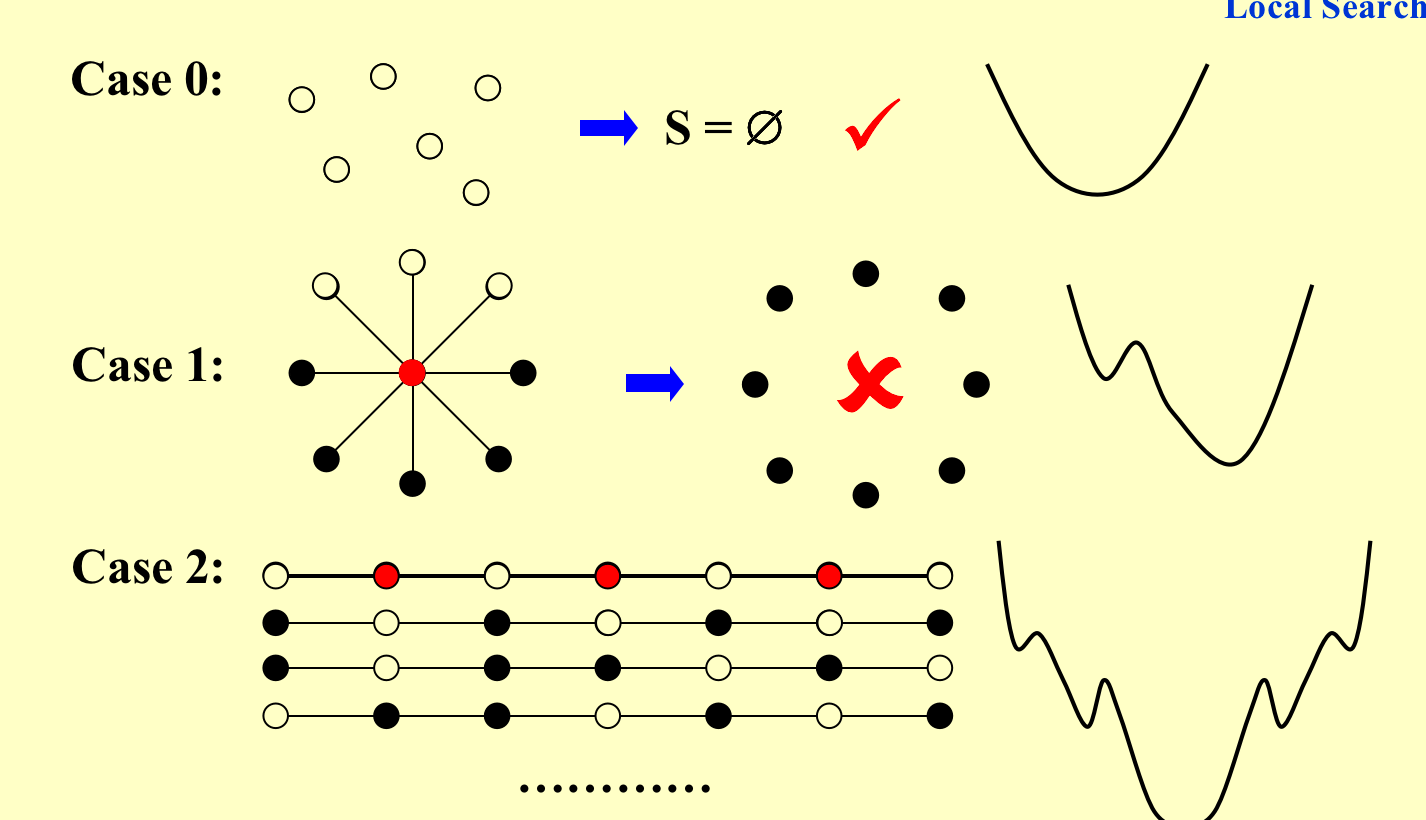
Metropolis算法
相比于原来的梯度算法,红色是改动的部分。我们随机选出来一个点,如果比当前的解要好,那么正常进行替换;如果更差的话,仍旧会有一定的概率替换成新的点。相比于原来的解,cost越大替换概率越低。
T如果特别大,那么替换概率为1,如果T特别小,那么就是原来的算法,替换概率几乎为0。随着算法的推进,替换概率越小越好,也就是T越小越好。
思考算法的结束时间,一种可行的想法是当概率小到某个阈值之下就结束。

Simulated Annealing 模拟退火算法
随着算法的迭代,越来越接近最优解,所以T越来越小(模拟温度降低),上升替换概率也越来越小。
3. Hopfield Neural Networks¶
相关定义
给定有权图,如果边的权重小于零,那么两个端点有相同的状态,如果权重大于零,那么两个端点有不同的状态。权重的绝对值越大,那么这条边越重要。定义好边和坏边(好边就是满足上述条件的边) \(w_es_us_v < 0\)。
对于一个顶点,如果其好边权重大于坏边权重则称之为满足结点。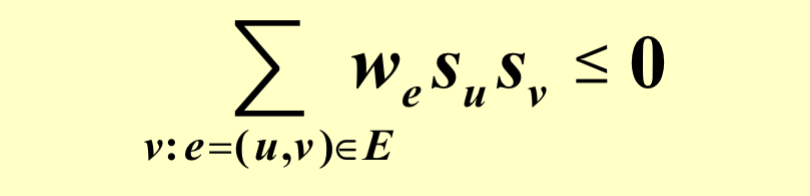
如果所有结点都是满足的,那么这个图就是稳定的。
State-flipping Algorithm
如果根本就没有一个可行解,那么这个算法就会死循环
ConfigType State_flipping()
{
//从一个随机的解开始
Start from an arbitrary configuration S;
while ( ! IsStable(S) ) {
u = GetUnsatisfied(S); //每次随机找一个不满足的结点
$s_u$ = - $s_u$; //把这个结点进行变色
}
return S;
}
下面证明:这个算法最多迭代所有边权绝对值的和次数,必定能够找到可行解。
我们把当前好边权重的绝对值的和记作函数,来衡量距离可行解的距离。我们希望这个值不断地增大。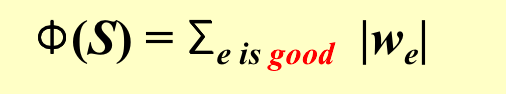
当我们改变一个结点的状态
而我们每次改变的点的状态是不满足的,所以每次迭代都是严格递增的,最多增加到所有边的边权和,这个时候所有的边都是好边。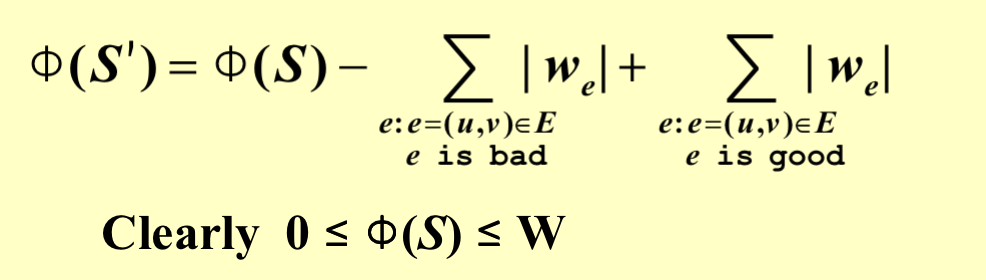
这个算法不一定每次都增加满足的结点,但是一定会增加好边的权重和。
思考这个算法的时间复杂度,因为权值可以很大,所以这是一个伪多项式时间复杂度算法
4. 最大切问题¶
问题概述:给定一个图,找到一种将其点分成两个集合A、B的方法,使得两端分别在A、B集合的边的权重和最大(也就是说A、B内部的边权重和最小)。
现实例子:我们现在有n门课,m位同学,每位同学有两门想上的课,现在我们要排课,使得能够同时参加自己最喜欢的两门的同学最多。我们以课作为结点,以人作为边,如果一个人喜欢某两门课,那么进行连线,现在给点染色,一个上午一下午。
构造local search的方案:
目标:最大化联结边的权重。 初始解:随机分组即可。 邻居:改变一个点的分组。
这其实就是Hopfield Neural Network问题的特殊情况,只是所有的边权为正。
我们还是按照Hopfield Neural Network问题的算法来解决最大切问题,这里的满足不满足变为——如果从某个节点出发到同集合的另外一个节点的所有边权和小于,从这个节点出发到另外一个集合的节点的所有边权和,那么称这个点为满足。但是我们需要额外思考几个问题。
上述方案找到的局部最优解不会比全局最优解的一半差。
对任意在集合A中的结点,从他出发另一端点也在A的边权和一定小于等于从他出发另一端点在B的边权和(如果大于,那么不是局部最优解)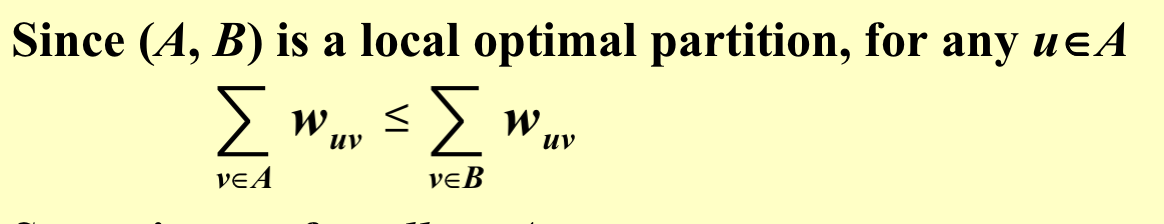
把A中的所有点加起来,那么就是两个点都在A的边的权重和的两倍(因为算了两次)小于等于端点跨越集合的边的权重和。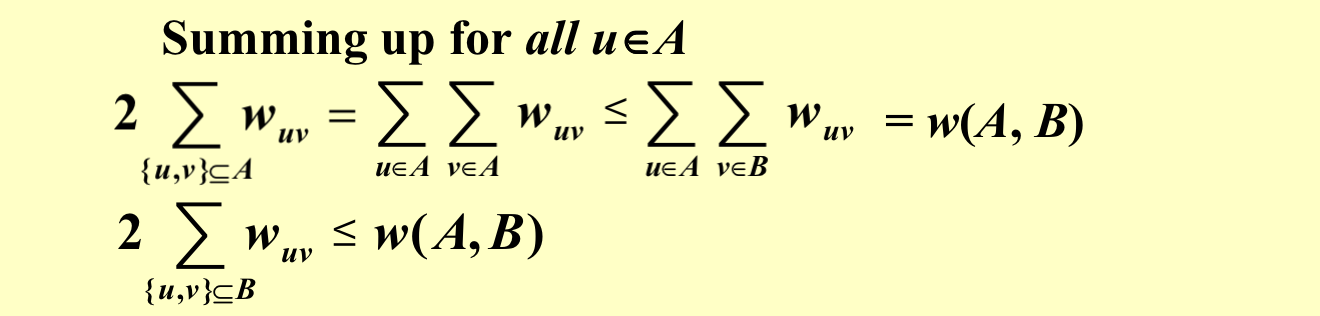
左边是最优解,最优解的上限是所有边的权重和。
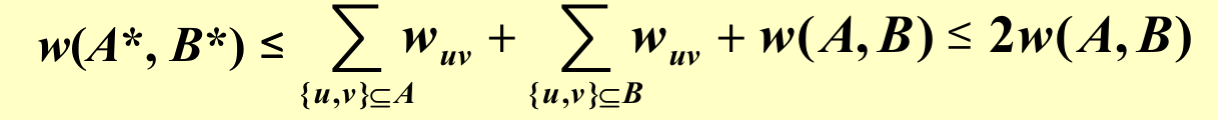
如上算法还是伪多项式时间复杂度(边权和x点的个数)的算法,我们是否能够改进这个算法呢?
我们尽可能寻找能够让我们割边(端点在不同集合的边)权重和增加更多的点来进行翻转

近似比原来是2,现在会变差为\(2+\epsilon\)。
原来我们只是去翻转一个节点,我们现在翻转k个节点来构成邻居。
我们先跟以前一样,翻转一个节点(这个节点翻转能使得割边权重和增加最多),之后在这个翻转的基础上再去翻转下一个节点,翻转k次,从这k次中,取出割边权重和增加最多的成为邻居。

5. HW¶


6. The End¶
Quote
- ADSNotes_Algorithms.pdf(from Carton手写笔记)
- ADS11ppt
- 小角龙(18)复习笔记.pdf
- 智云课堂:2023yy
- JerryG(20)复习笔记.pdf
评论
本文总阅读量次