5.Binomial Queue
约 826 个字 16 张图片 预计阅读时间 3 分钟
1. Definition¶
- target:左式堆将插入、合并和删除最小元的操作控制在\(O(logN)\),尽管时间已经够少了,但二项队列进一步降低了这个时间。二项队列(binomial tree)以最坏时间\(O(logN)\)支持合并和删除,并且插入操作平均花费常数时间。
- 二项队列不是一棵树,而是树的集合,称为森林,这里的树有特定的形式,同时也具有堆序性,叫做二项树(binomial tree)。如图为一个二项队列,有B0, B1, B2, B3, B4五棵二项树。可以看到,二项队列具有以下特性:
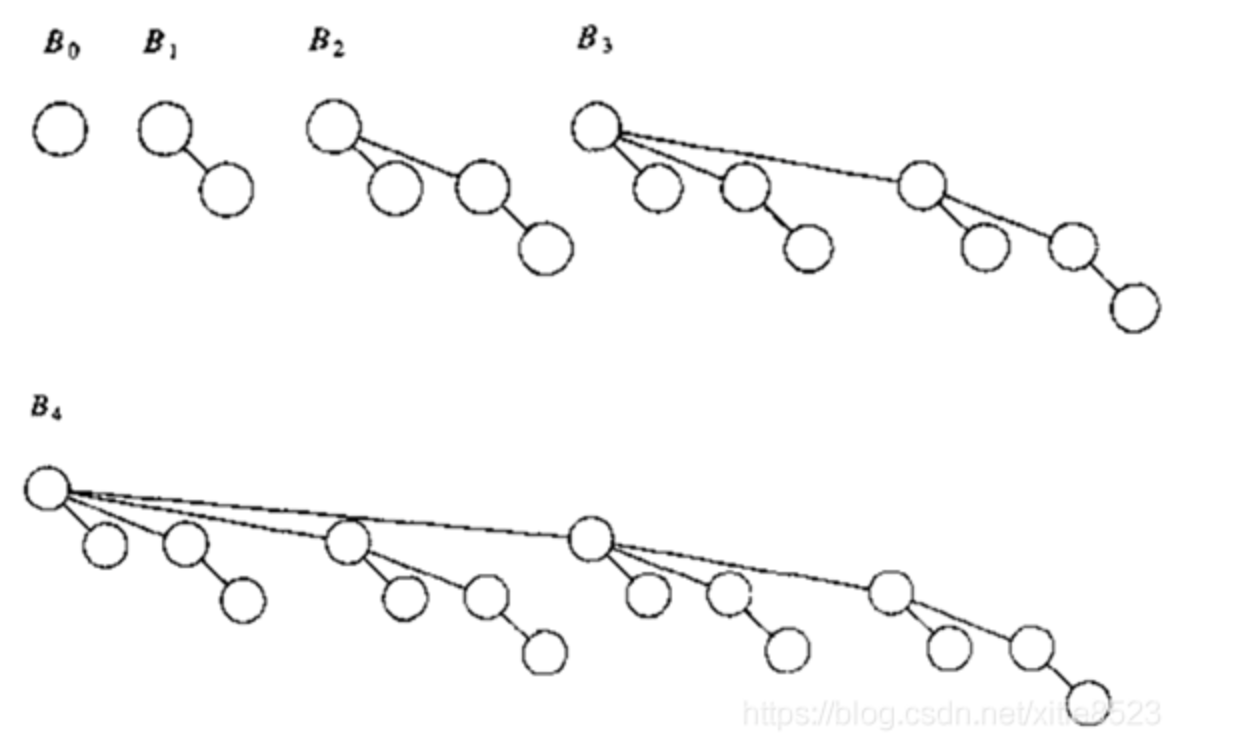
- 高度为k的二项树\(B_k\)通过将高度为\(B_{k-1}\)的二项树接到另外一棵高度为\(B_{k-1}\)的二项树的根上构成;
- 二项树\(B_{k}\)由一个带有儿子\(B_0\),\(B_1\)·····\(B_{k-1}\)的根组成(形状上),从\(B_{k}\)的构成过程可以知道这个特性,在构成\(B_{3}\)的过程中,经历了根节点接上\(B_{0}\),\(B_{1}\),\(B_{2}\)的过程;
- 高度为k的树有\(2^k\)个节点,第k棵树的节点会等于第k-1棵树的节点乘2;
- 对于每个\(B_k\),深度d处的节点数为二项系数\(C_k^d\);
2. Operations¶
2.1 FindMin¶
- 最小的值就在根中,而根最多有\(logN\),所以时间复杂度\(O(logN)\);
- 我们可以跟踪记录最小的根,那么时间复杂度就变成了\(O(1)\);
2.2 Merge¶
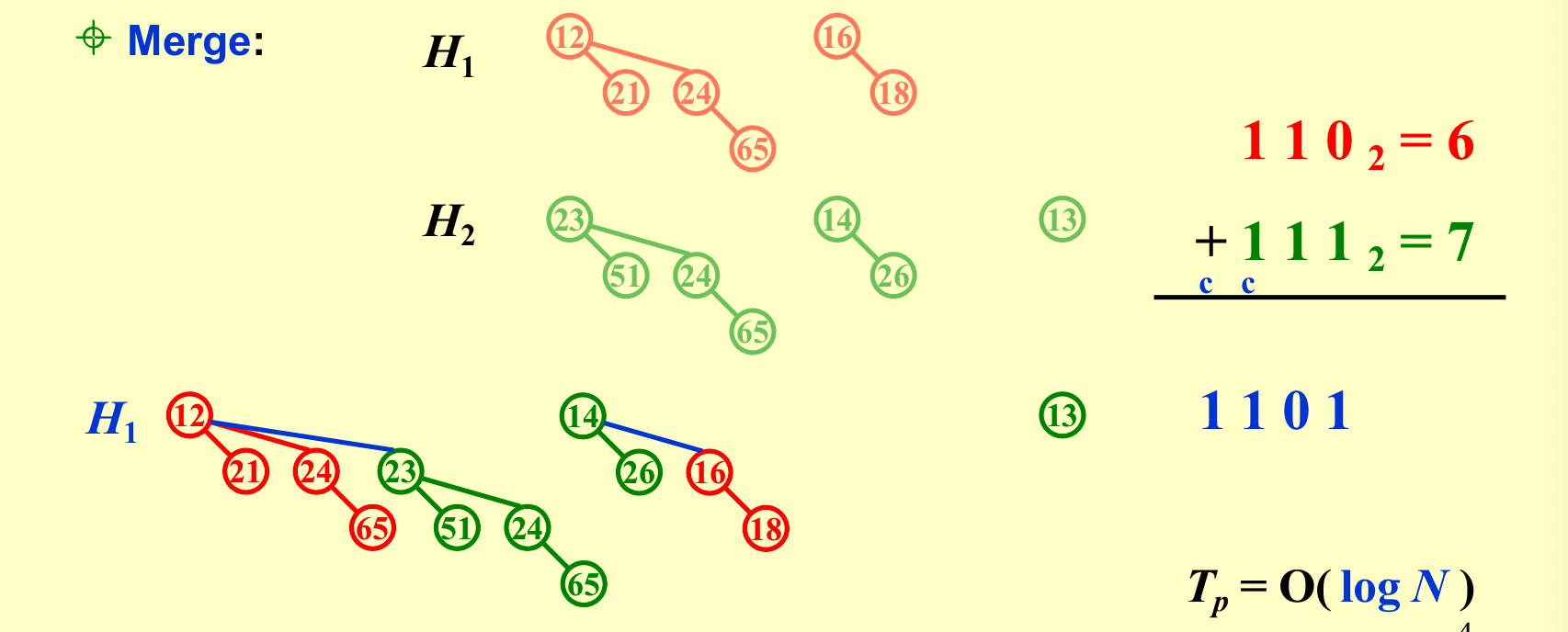
- Must keep the trees in the binomial queue sorted by height;
- 时间复杂度为\(O(logN)\);
2.3 Inset¶
- 可以看成是特殊情况的merge;

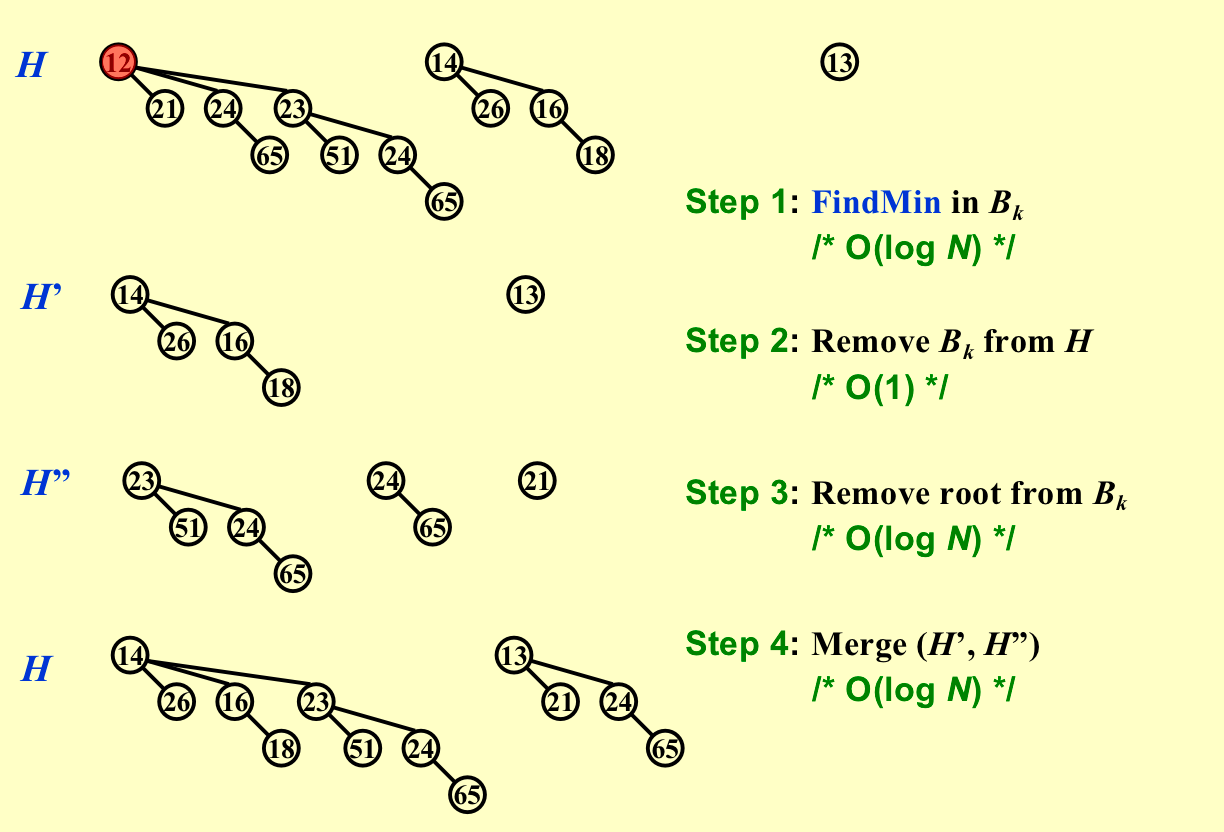
2.4 DeleteMin¶
2.5 Decrease key¶
-

-
减少key的值,这样的话为了保持堆的有序性,要不断地与父亲进行比较交换,时间复杂的为\(O(logN)\);
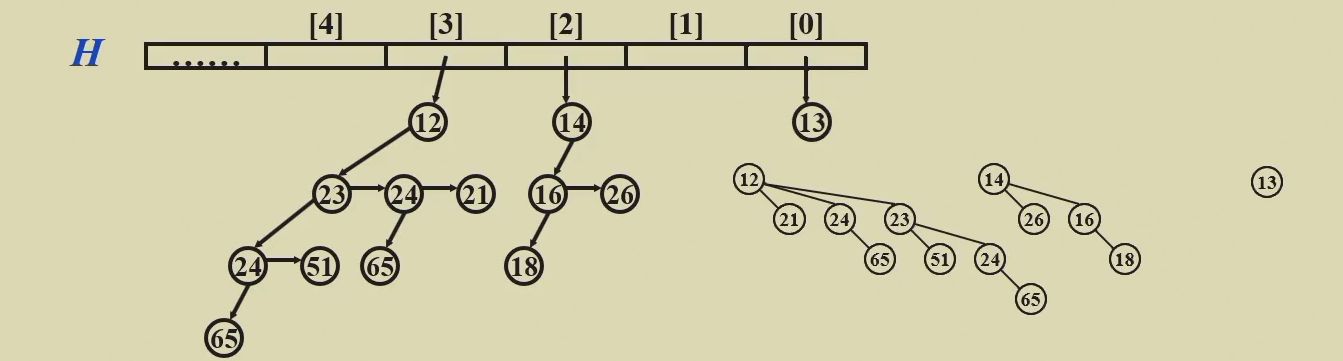
3. Implementation¶
| 操作 | 性质 | 解决方法 |
|---|---|---|
| DeleteMin | 要快速找到所有的subtree | 用链表实现Left-child-next-sibing |
| Merge | 孩子要跟据大小进行排序 | 新的树一定是最大的,以此来维持大小排序; |
数据结构
注意注意,真正实现二项树使用firstchild-nextsibling的方法!这里的编程细节比较多,容易出填空题啥的......反正这些算法实现都挺重要的!


两个感叹号可以把任何一个数转化成1或者0;


4. 摊还分析¶
- A binomial queue of N elements can be built by \(N\) successive insertions in \(O(N)\) time.
Proof1(Aggregate normal)
- 如图所示,step表示插入代价,link表示连接代价,link其实就是进位;
- 所以总的step代价就是n,link代价其实也是\(O(n)\),得证;

- 观察,发现,插入代价越小,树的数目就会增加;
- 代价为1,数目加一;代价为2,数目不变,代价为3,数目减一……

Proof1(Aggregate yds)
- 如果最后一个树是0,那么cost就是1,如果倒数第二颗树是0,那么cost就是2,这样子以此类推……
- 所以最后是0的有n/2个,最后是01结尾的有n/4个……
-
然后加起来就对了;
-

Proof2
- 根据树的变化数目就是2-cost;
- \(C_i\) 表示第i步插入的实际cost,\(φ_i\) 表示经过第i步插入后树的数量;
-
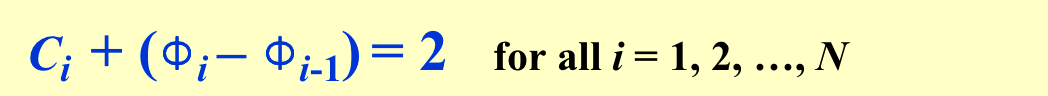
-

-
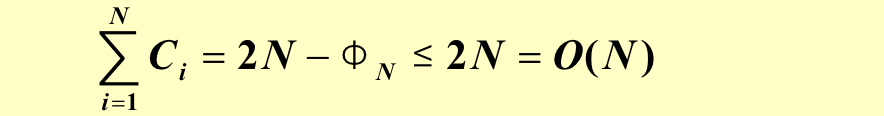
参考资料
- ADS05ppt
- 智云课堂:2022yds,2023wc
- 小角龙(18)复习笔记.pdf
- JerryG(20)复习笔记.pdf
评论
本文总阅读量次