6.Backtracking
约 605 个字 19 张图片 预计阅读时间 2 分钟
1. 引入¶
- 找到问题答案的一个可靠方法是列出所有候选答案,检查每个答案,宣布确定的答案。
- 回溯使我们能够消除对大量候选人的明确检查,同时仍然保证在算法运行到终止时会找到答案。
- 基本思想是假设我们有一个偏解(\(x_1\),··,\(x_i\)),然后我们加一个解进去,并检查(\(x_1\),··,\(x_i\),\(x_{i+1}\))是否满足约束。如果答案是“是”,我们继续添加下一个\(x\),否则删除这个\(x\),回溯到先前的部分解(\(x_1\),··,\(x_i\))。其实就是深度优先算法。
2. 八皇后问题¶
-
在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
-
以四皇后为例
3. 道路重建问题¶
通过给定的点集来回推原来的坐标;
例子¶
只要每次选最大的点,那么比较的对象永远是两边的端点!


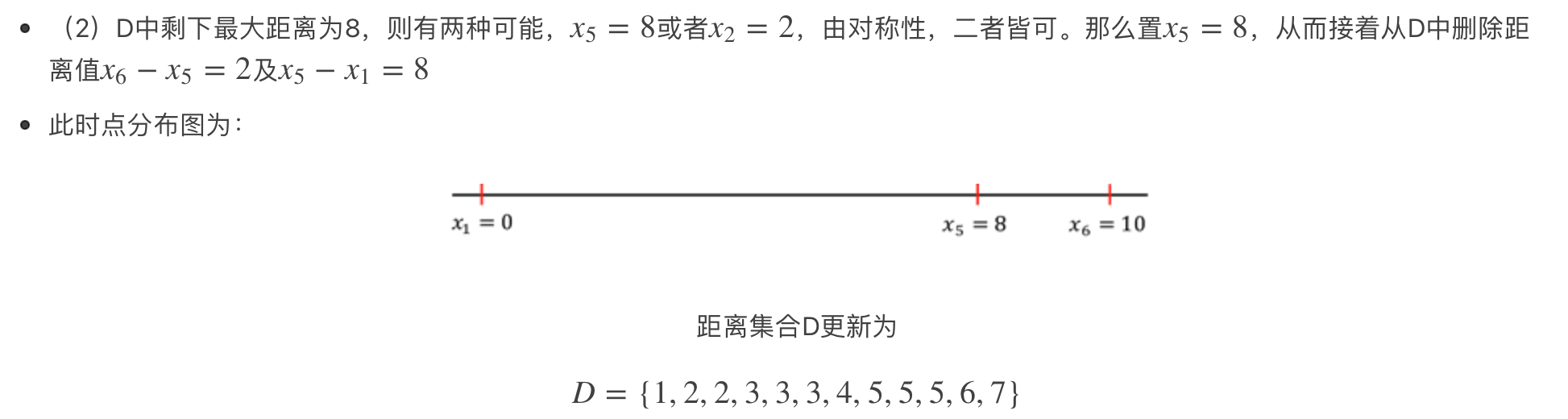


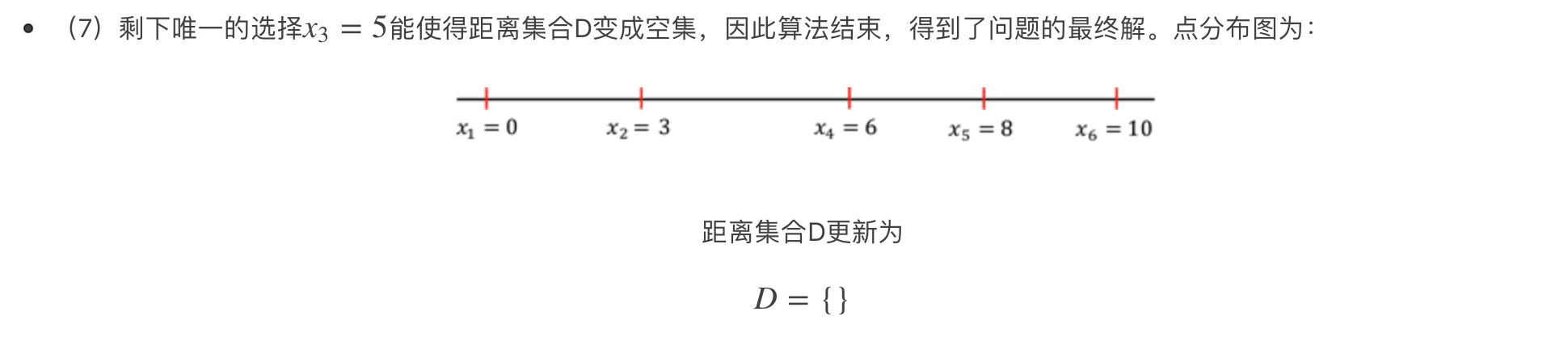 决策树
决策树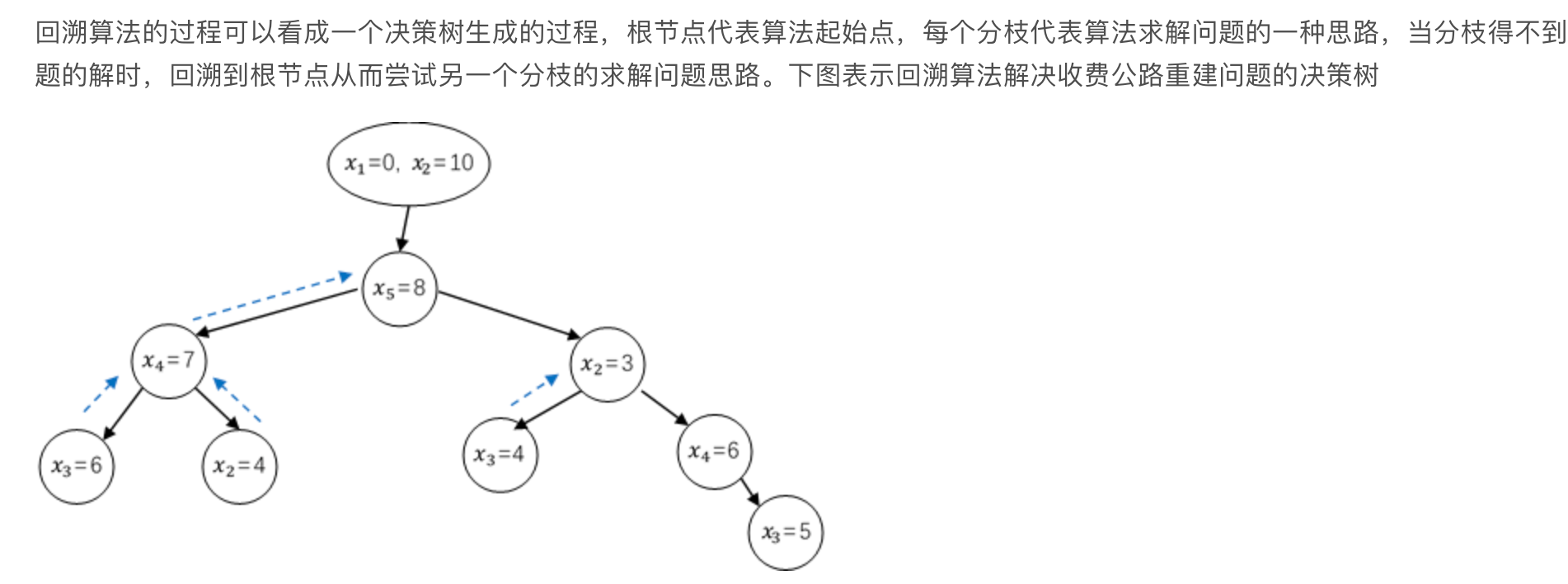
伪代码¶


4. Backtracking 代码思路¶

类别数更少的情况放在前面判断!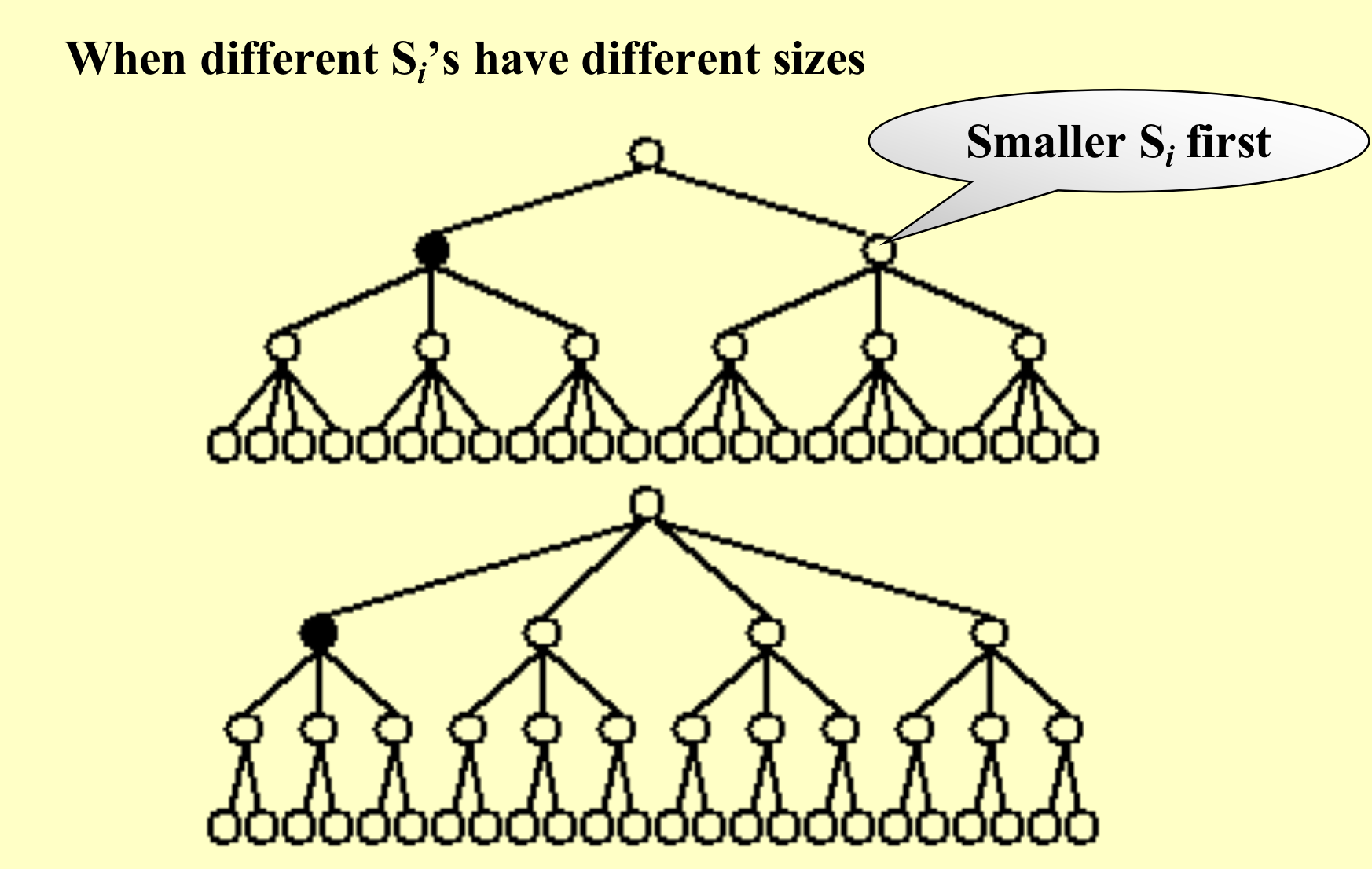
5. AlphaGo¶
井字棋
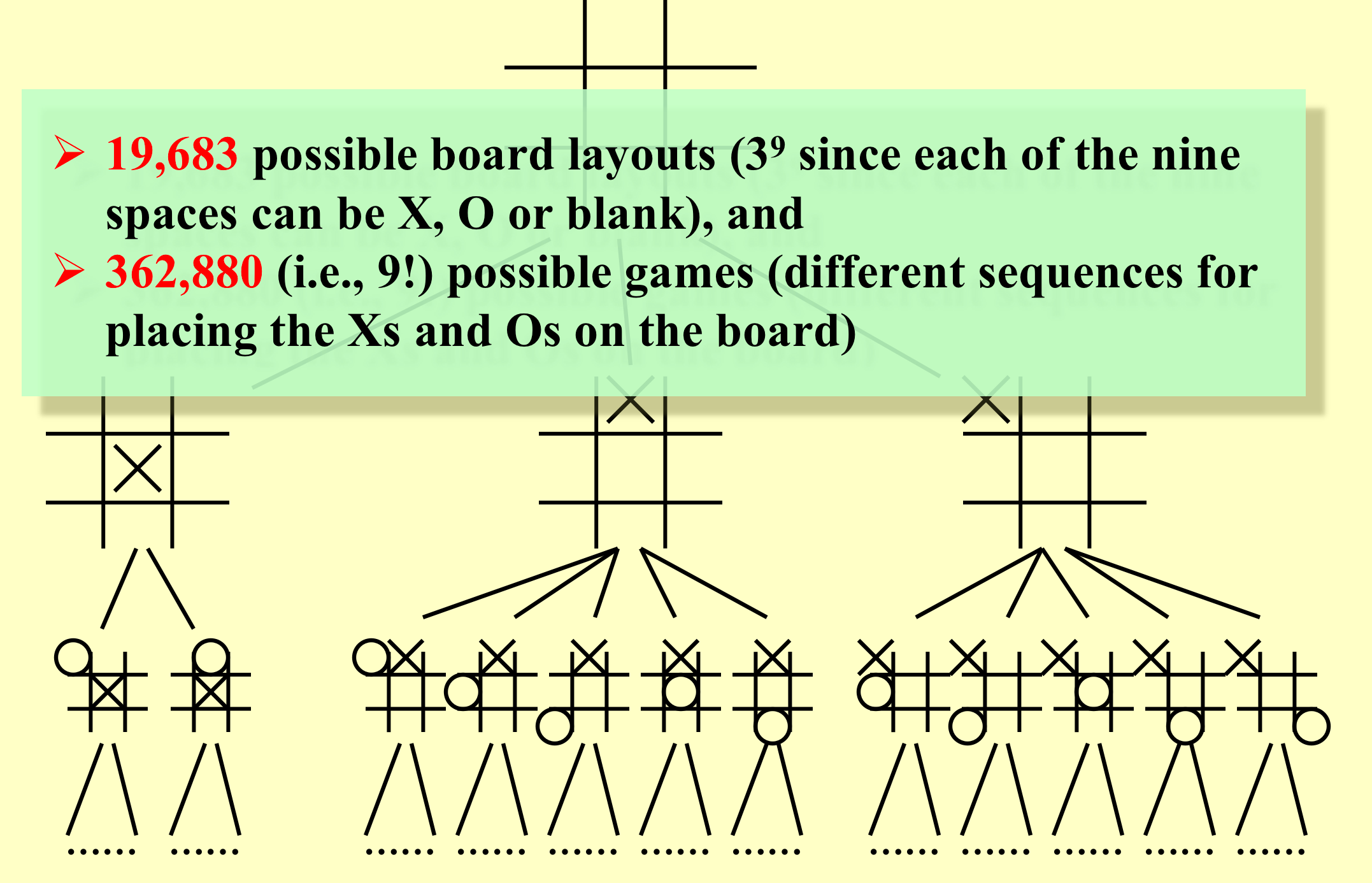
采用Minimax Strategy
- 使用状态评估函数来估,
f(P)=W(computer)-W(human),W( )表示这一情况下,获胜的可能状态,所以计算机需要让他尽可能的大; -
如图,圆圈有四种可能性赢,而叉有六种可能性赢;(2023yds)
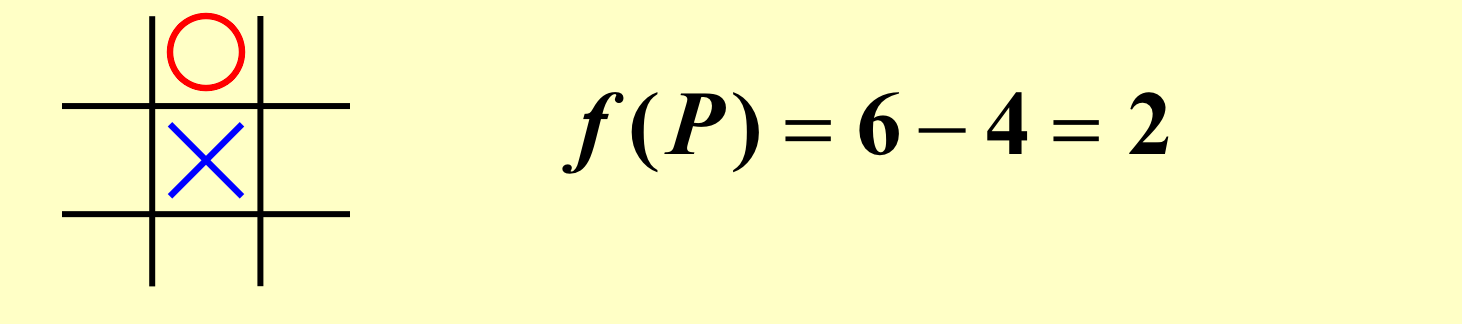
-
计算机要让f()最大,人要让其最小;
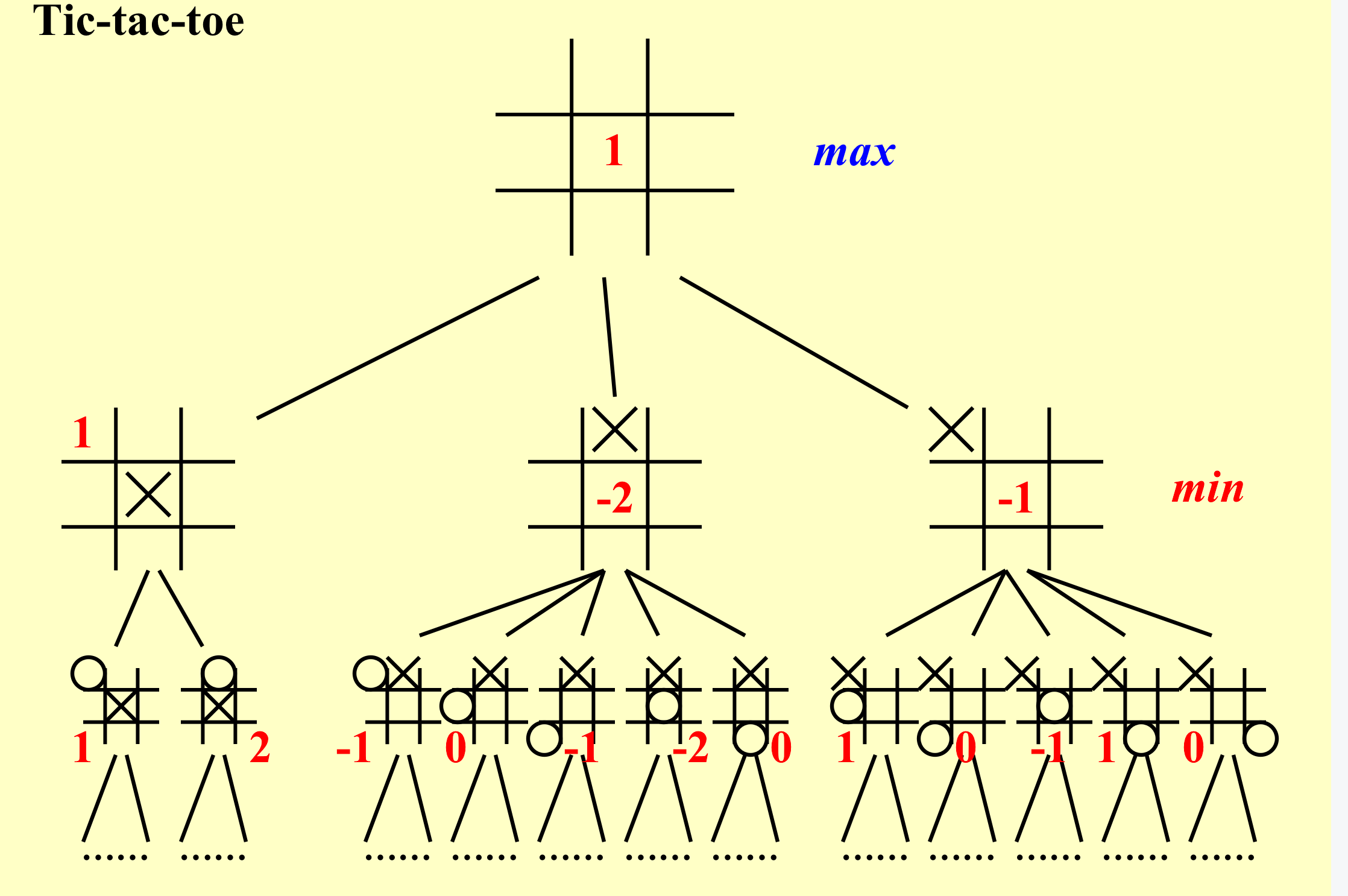
6. αβ剪枝(αβ pruning) -> 重要¶
from JerryG
常见于棋类算法中,或者说博弈类问题中,但其思想是剪枝的条件不止跟当前节点有关,而且跟上层或同层中的、已遍历过的节点有关。或者说,可以利用已经遍历的节点带来的信息,来帮助排除不必要搜索、进行剪枝。

- 不管黑色的地方取什么都没有意义;
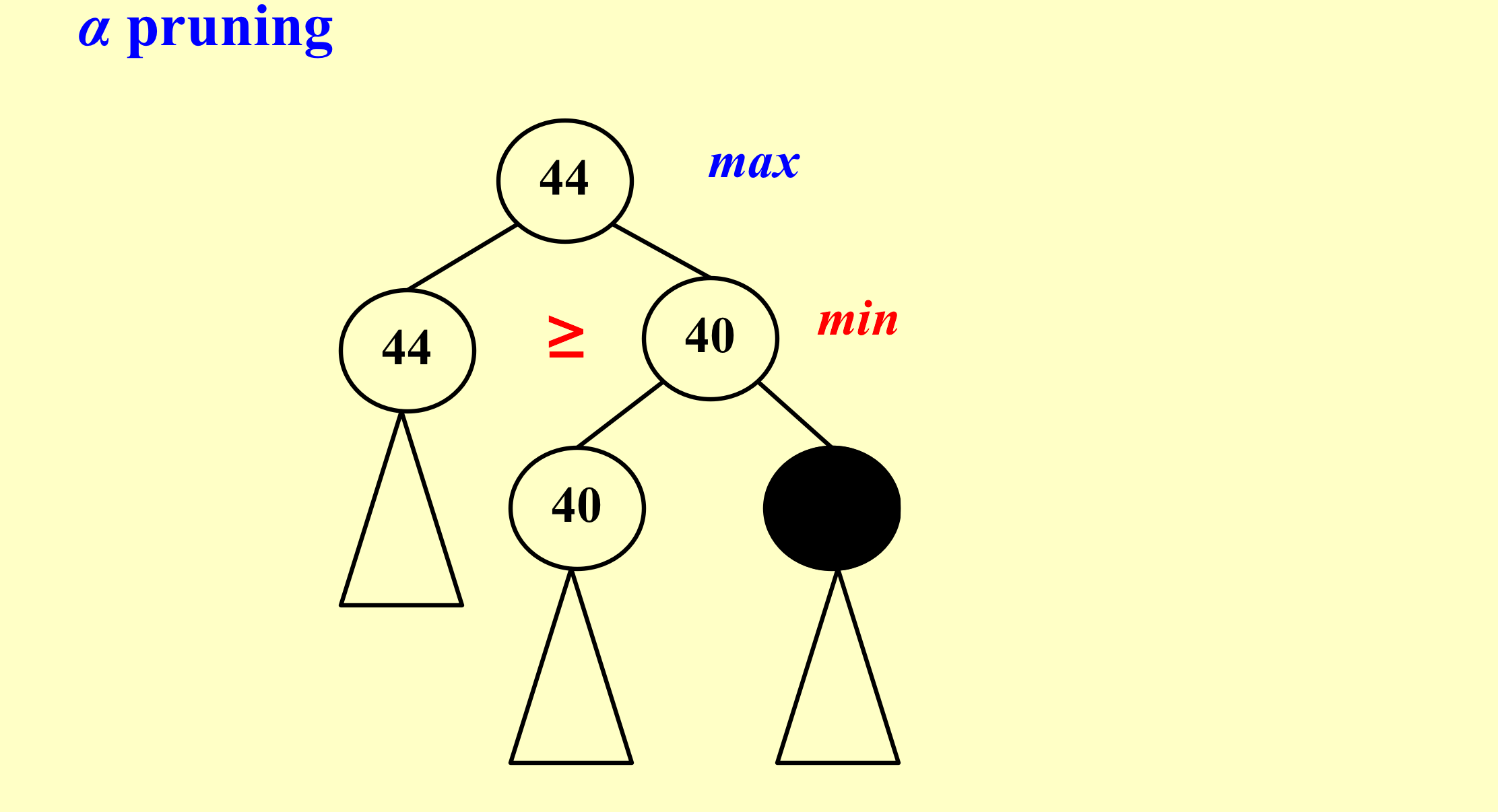
-
不管黑色的地方取什么都没有意义;
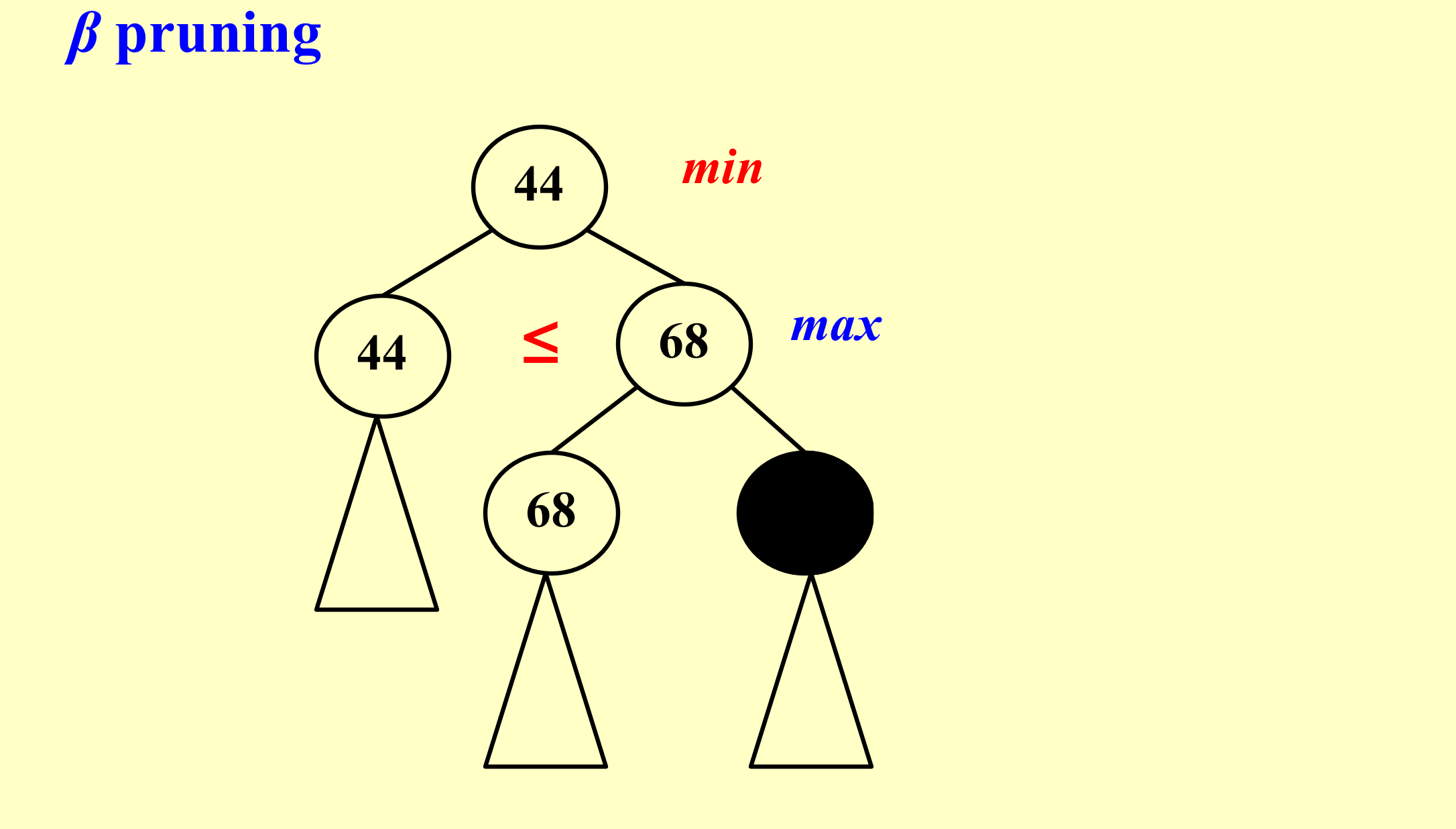
-
注意遍历的顺序是先从左往右、再从下往上的,二叉树中,被剪掉的节点往往是右节点。
- 搜索的点可以变成\(O(N^{0.5})\);
参考资料
- ADS06ppt
- JerryG(20)复习笔记.pdf
评论
本文总阅读量次