7.Divide and Conquer
约 1112 个字 26 张图片 预计阅读时间 4 分钟
1. 概述¶
General recurrence: T(N) = aT(N/b) + f(N)把问题分成a个子问题,每个子问题的问题规模为原来的1/b,合并的时间复杂度为\(f(N)\),如上公式就是这个意思。
一些可以被divide and conquer解决的问题:
- The maximu m subsequence sum 连续的子序列的和最大值 – the \(O(NlogN)\)solution
- Tree traversals (树的遍历)– \(O(N)\)
- Mergesort and quicksort – \(O(NlogN)\)
combine对算法的时间复杂度的影响:
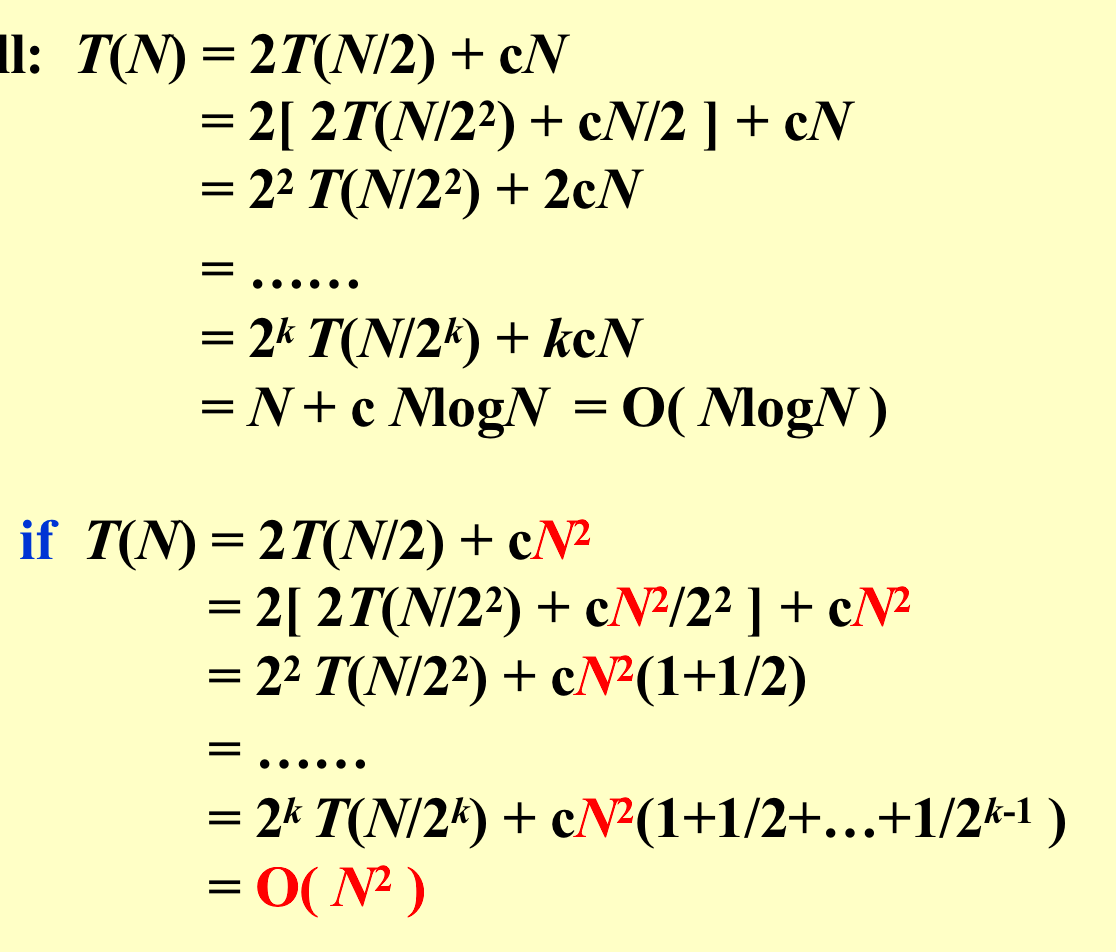
注意点(from JerryG)
- 分解成的不同子问题之间在各自的解决上必须互无关联,即形式上可以作为原问题的规模更小的 instance。子问题不能需要自身不包含的信息才能解决, 否则无“分治“可言。所以要定义好子问题,保证其独立性。
- 要想好如何根据小问题的解合并成大问题的解,这步同样不能复杂度太高。
- 对于足够小的子问题,可能直接解决比继续划分效率更高,如快速排序在子数列足够小时用普通排序方法速度更快。
- 分治法应用极其广泛,但并不是所有问题都能应用分治思想,尤其是全局内部关联度非常高的问题,比如棋类博弈问题。
2. 最近点对问题¶
问题背景¶
在应用中,常用诸如点、圆等简单的几何对象代表现实世界中的实体。在涉及这些几何对象的问题中,常需要了解其邻域中其他几何对象(最接近)的信息。例如,在空中交通控制问题中,若将飞机作为空间中移动的一个点来看待,则具有最大碰撞危险的2架飞机,就是这个空间中最接近的一对点。这类问题是计算几何学中研究的基本问题之一
具体方法¶
已知集合S中有n个点,使用分治法的思想就是将S进行拆分,分为2部分求最近点对。算法每次选择一条垂线L,将S拆分左右两部分为SL和SR,( L一般取点集S中所有点的中间点的x坐标来划分,这样可以保证SL和SR中的点数目各为n/2 否则以其他方式划分S,有可能导致SL和SR中点数目一个为1,一个为n-1,不利于算法效率,要尽量保持树的平衡性 )
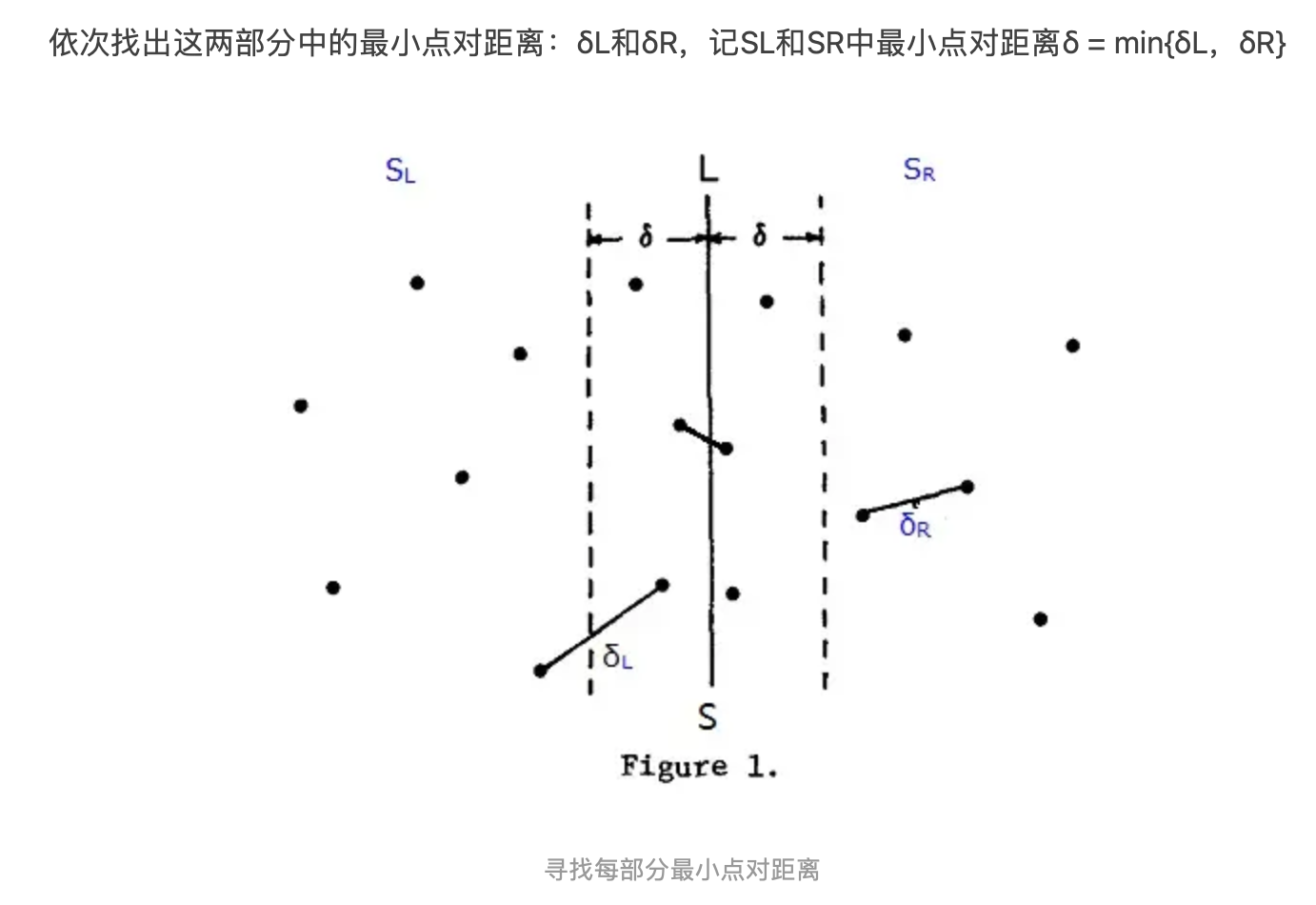
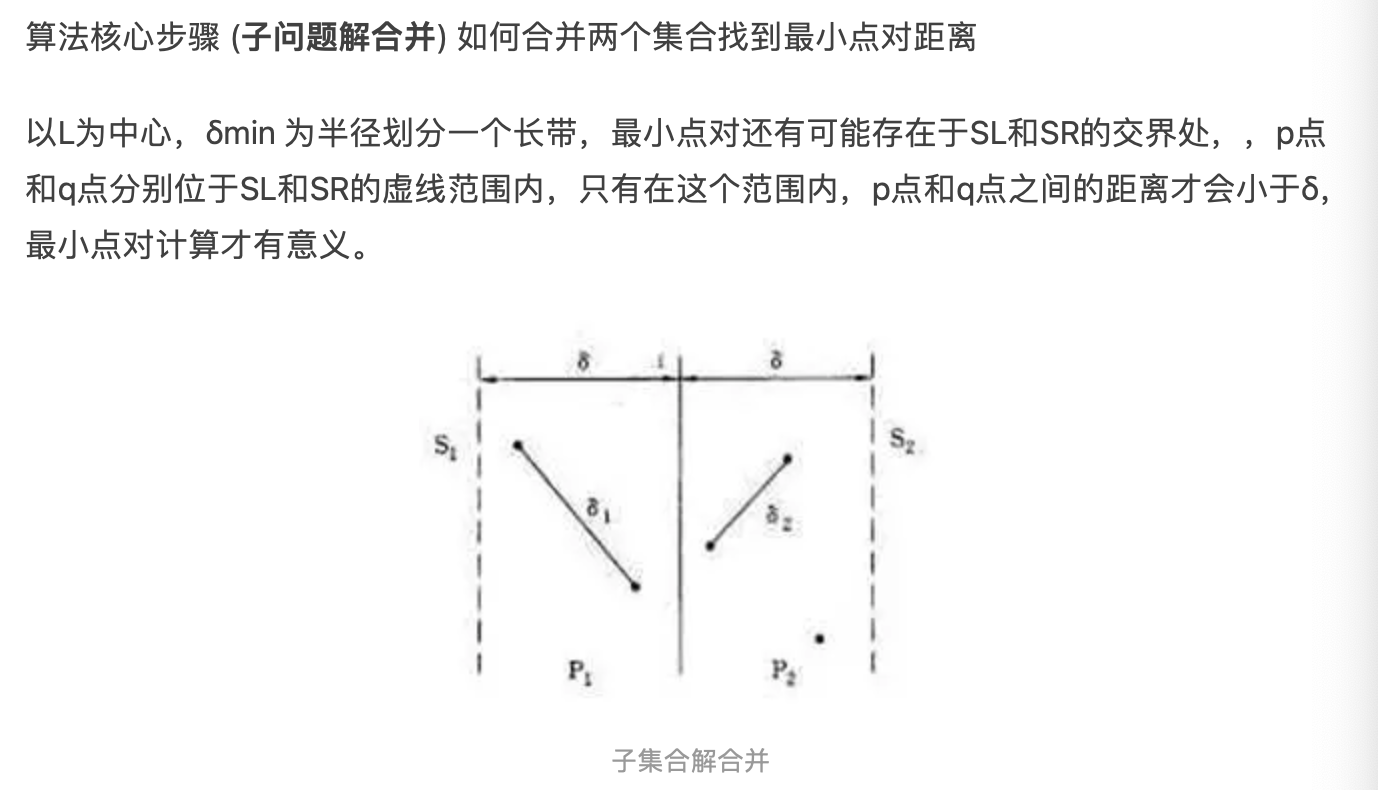

具体算法¶
- 如果只有两个点,那么直接输出;
- 根据横坐标,分成两个组,分别调用,求出两边各自最小的距离;
- 求出两边最小的距离a;
- 求出距离中心线a内的所有点,然后根据y坐标进行排序生成点对数组ptr;
- 对ptr中的每一个点进行遍历(包括左右!)
- 如果是中心线右边的点,直接跳过;
- 只需与相邻的6个点进行比较;

3. 分析¶
三种分析时间复杂度的方法:代入法(数学归纳法)、递归树方法(猜一个好的结果)、Master method(主定理)法;
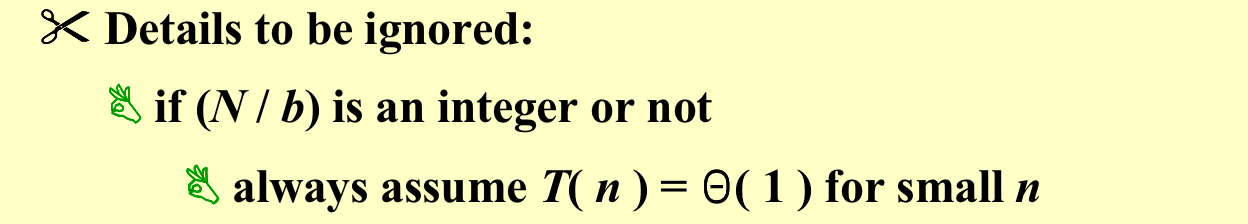
3.1 代入法示例¶
T( N ) = 2 T( [N / 2] ) + N(向下取整)

 必须得是cN,不能是(c+1)N,所以不行;
必须得是cN,不能是(c+1)N,所以不行;
3.2 递归树方法¶
找规律,一直分解到最后一层
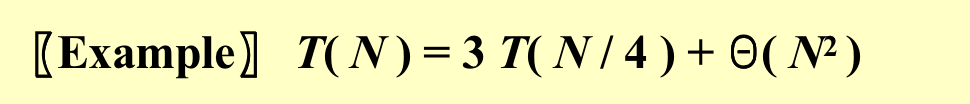
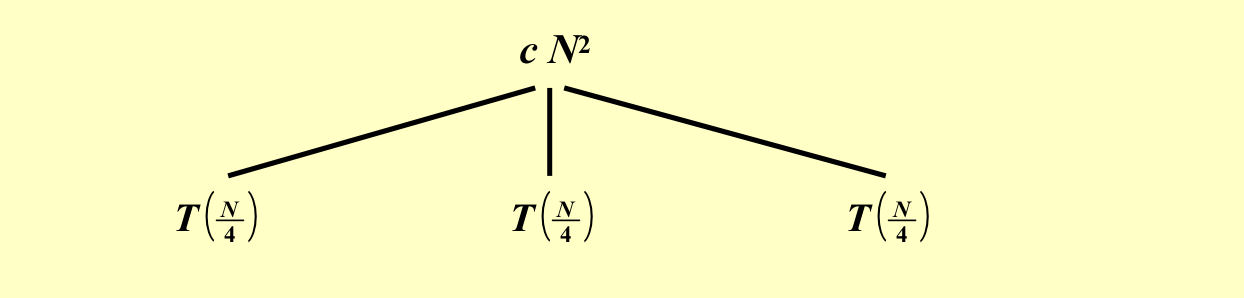
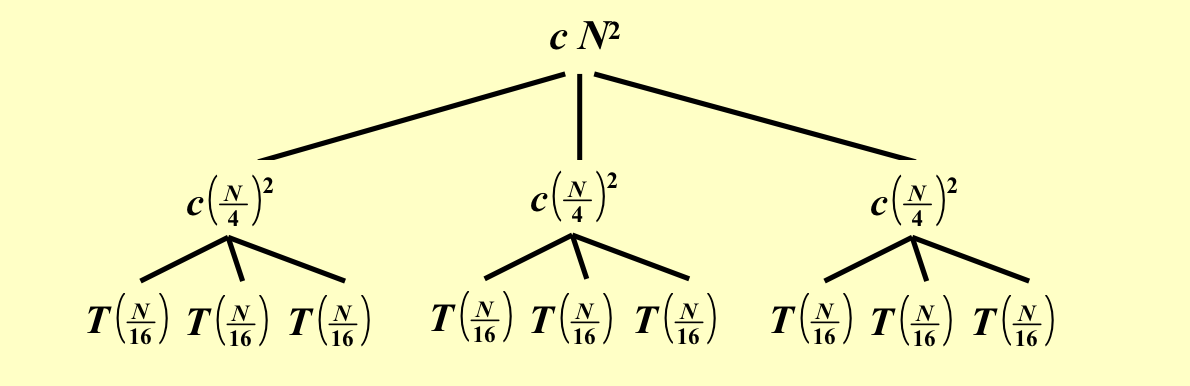
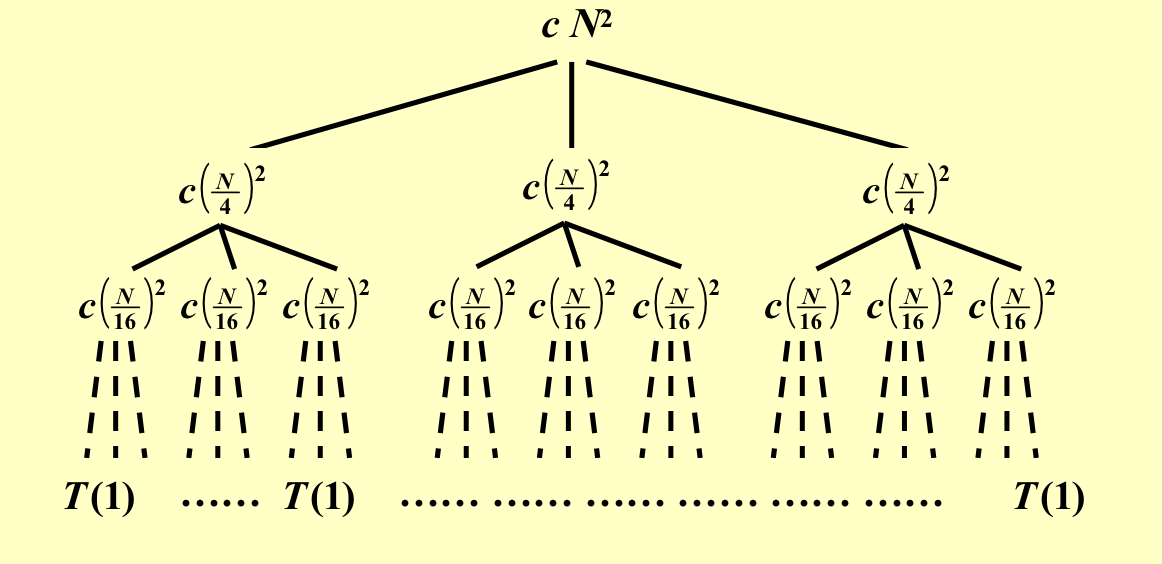
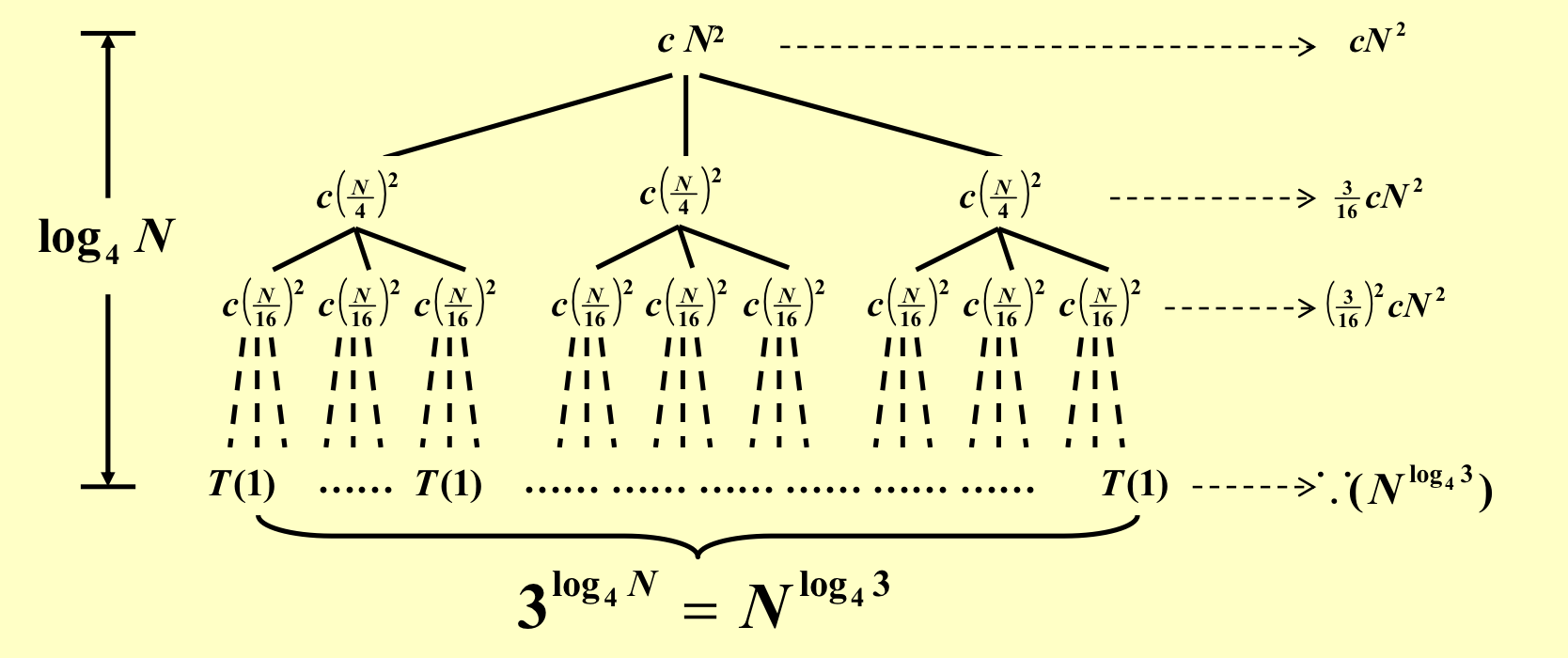
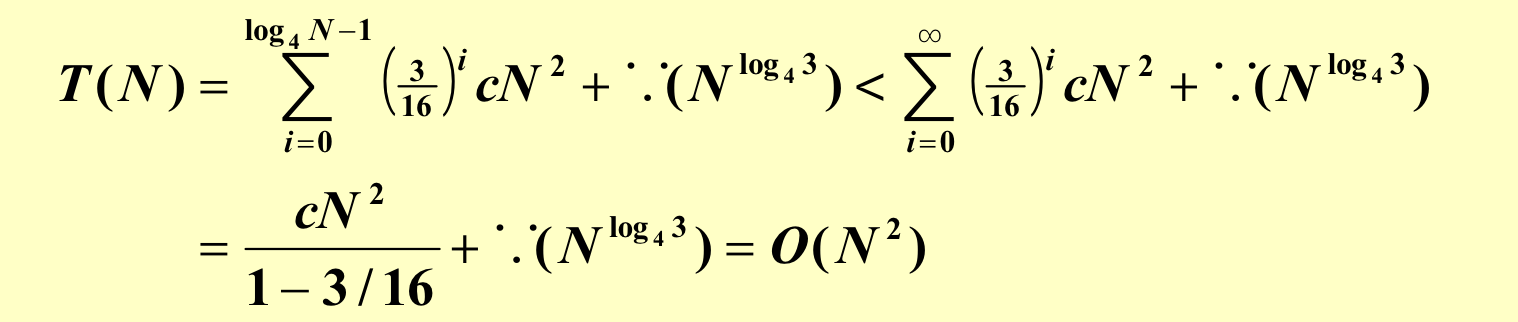
再来一个例子:
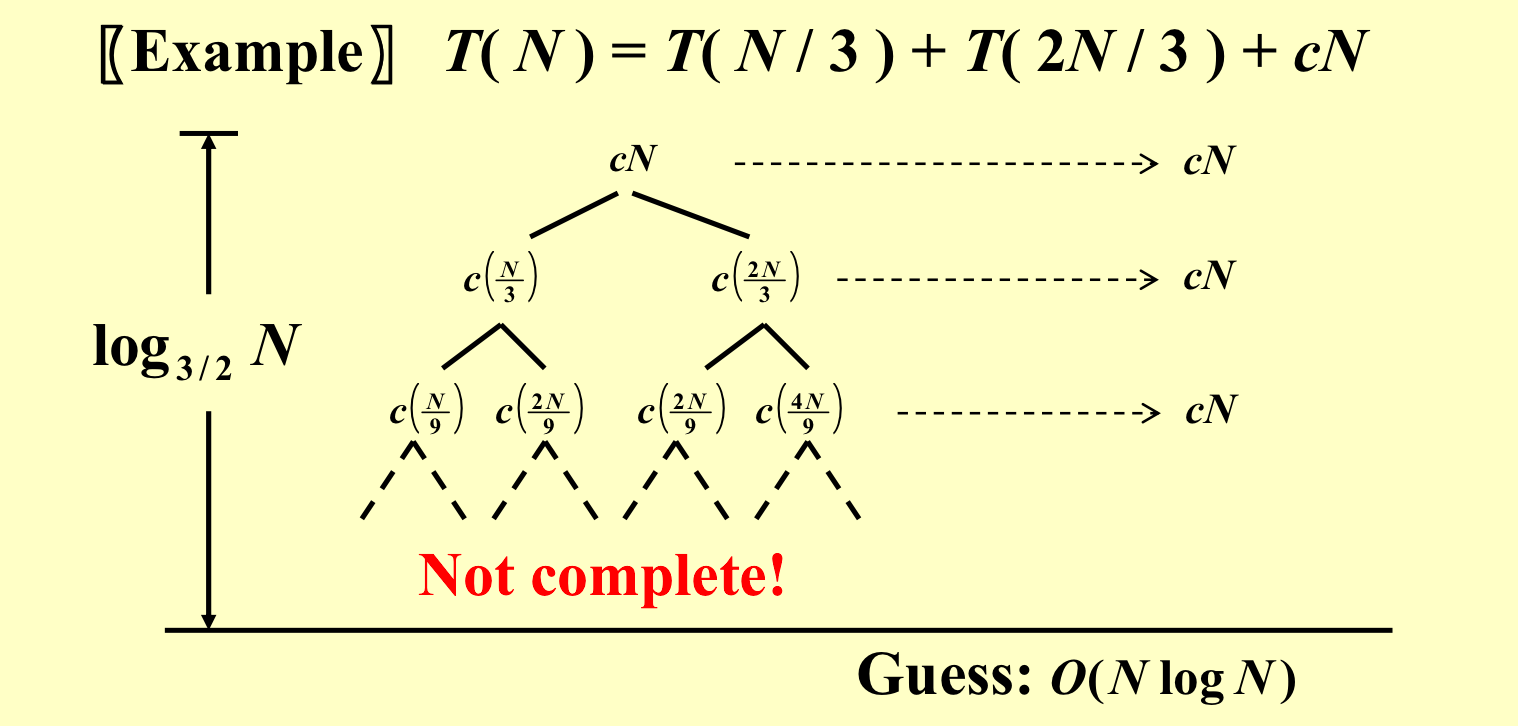
再利用归纳法进行证明
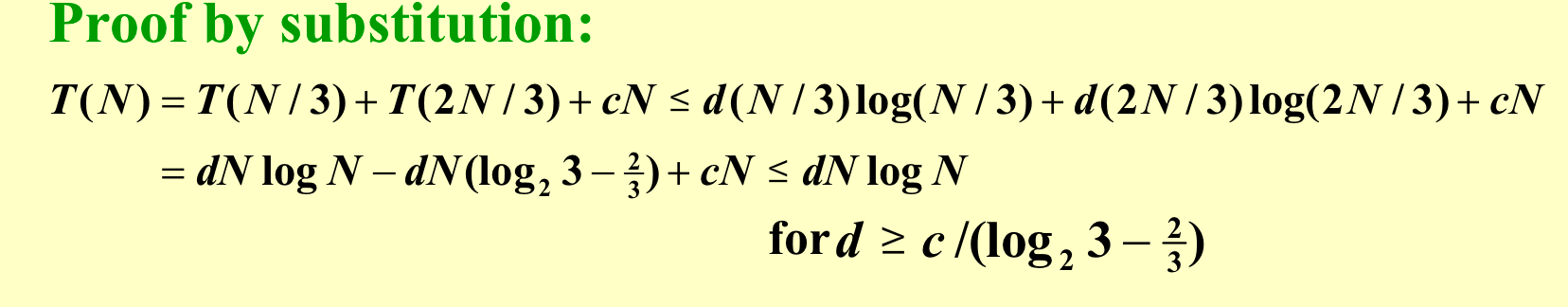
3.3 Master method¶
叫作主方法的原因是它分析的是 combine 和 conquer 部分哪个是主导。

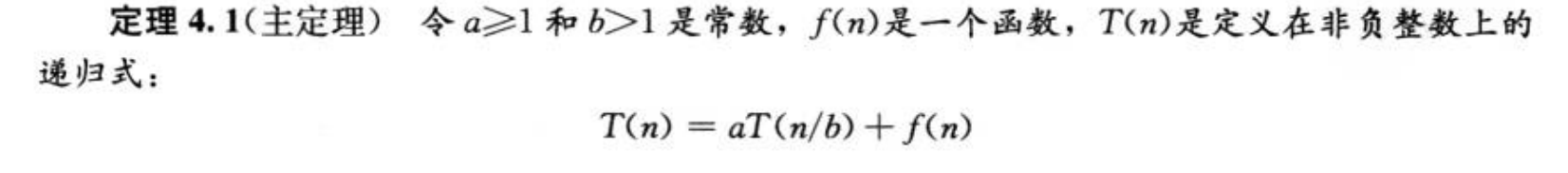

其实就是比较f(N)和 \(N^{log_ba}\) 的大小关系,第一种情况是后者大,那么就以后者为主;第二种情况是渐进意义上的相等;第三种情况是,前者比较大,而且满足一些关系,那么就以前者为主。
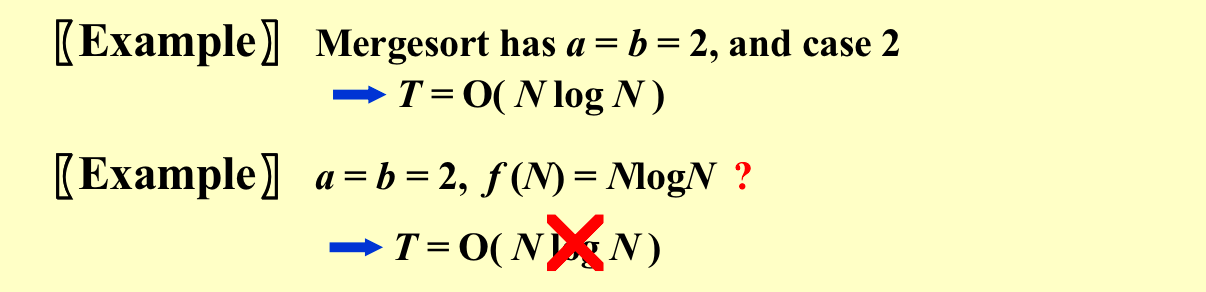
后者不满足case3的第二个条件
证明
此定理可以通过递归树进行证明
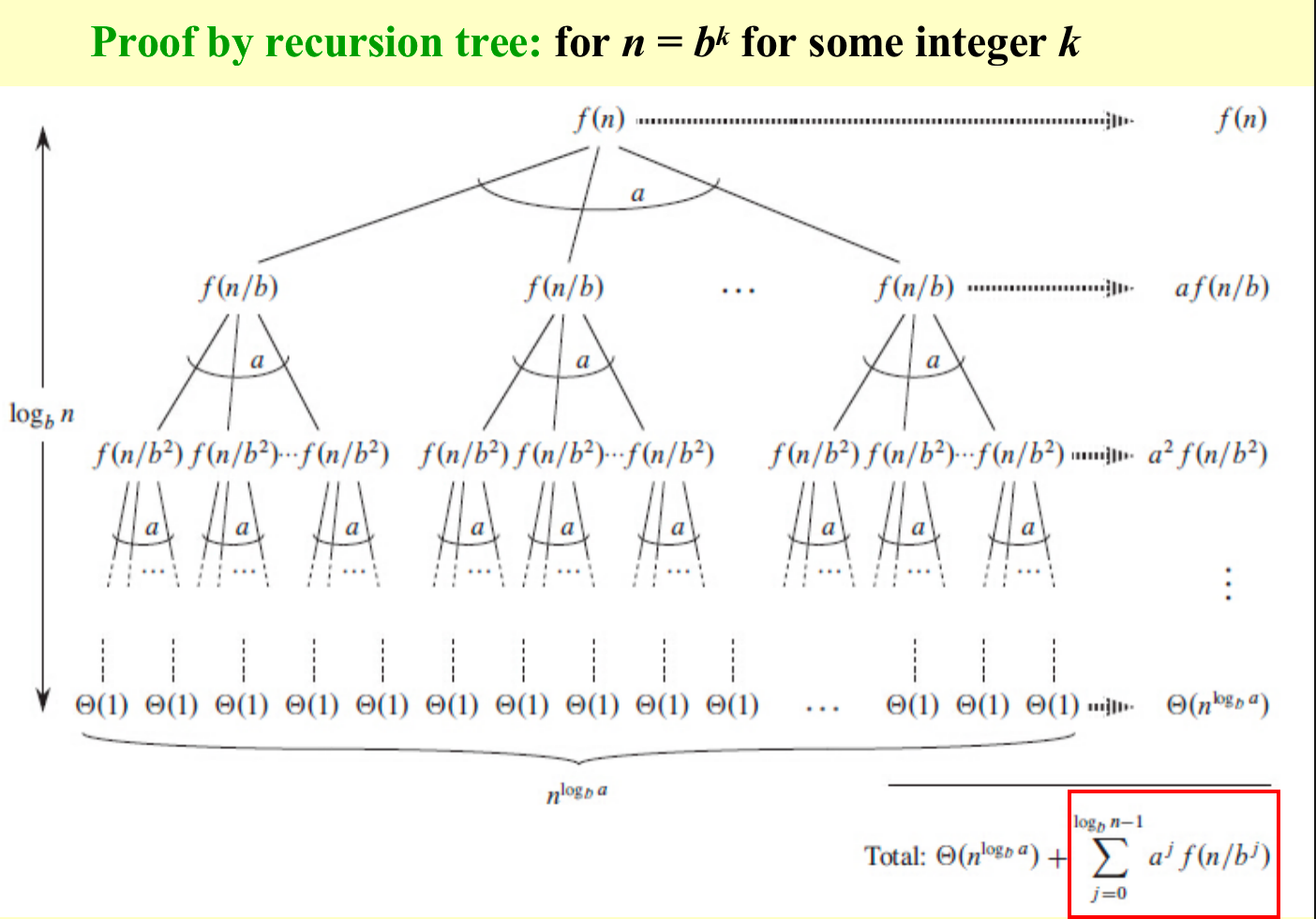
case1证明:
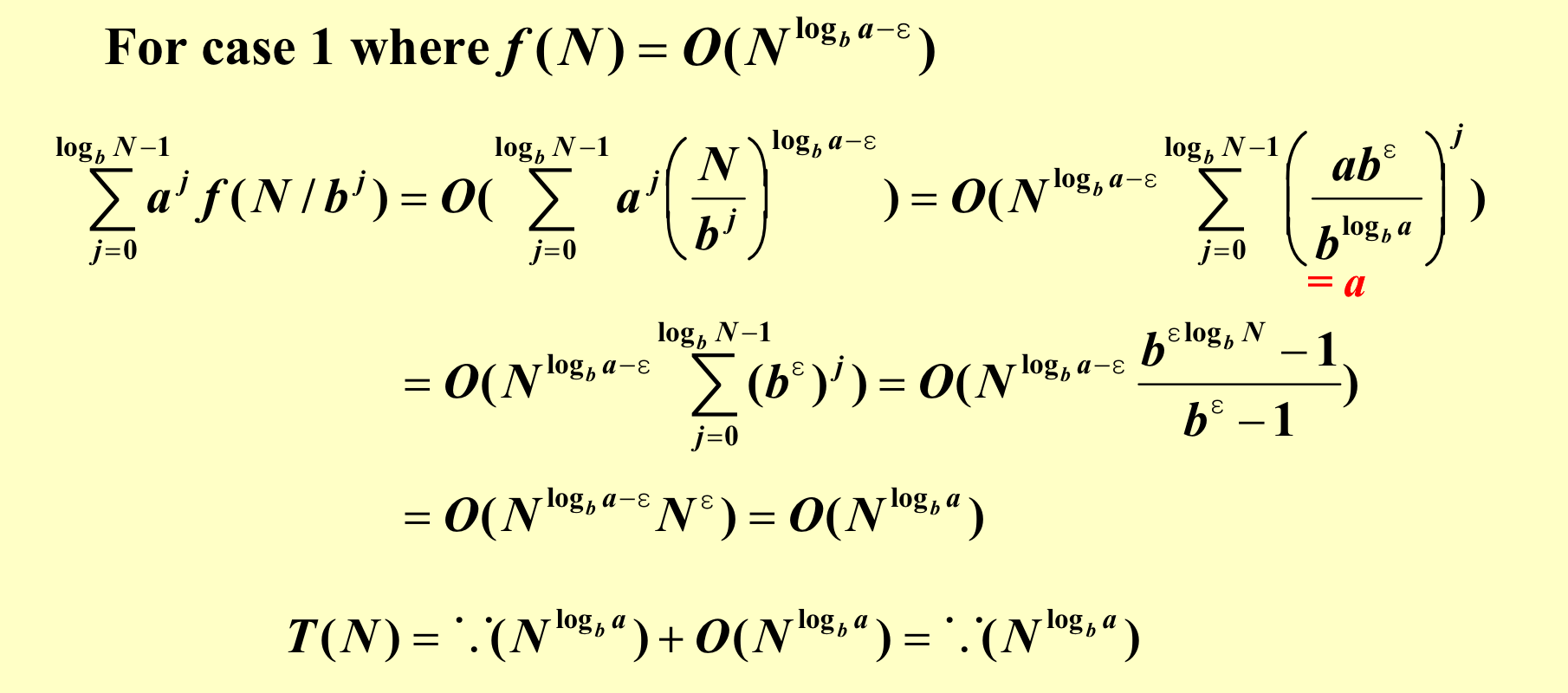
case2 和 case3 的证明看书。
另一个形式:

前面那个可以证明,但这个不能证明
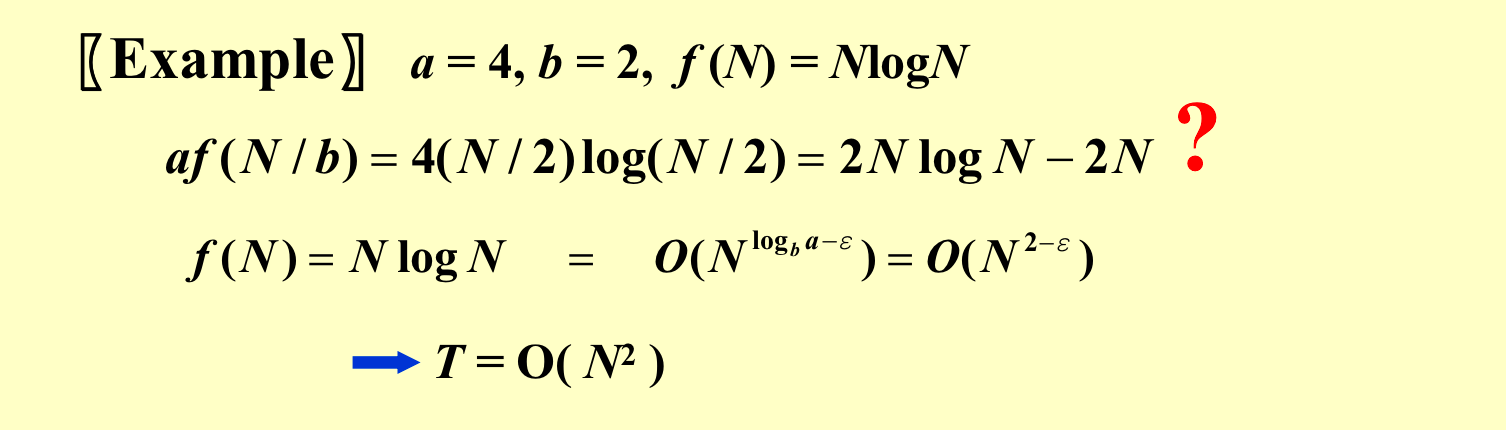
最强大的定理:
速记
递归递归产生的复杂度是 \(N^{log_ba}\), 这个指数 \(log_{b}a\) 跟 k 做比较,更大的一方显然可以主导复杂度。如果两者相等,给 f 的 log 的指数加一作为补偿。

参考资料
- ADS06ppt
- JerryG(20)复习笔记.pdf
- 智云课堂: 2022bjj,2022yds
评论
本文总阅读量次