跳转至

8.Dynamic Programming

约 1377 个字 16 张图片 预计阅读时间 5 分钟

0. 概览

  • 如果设计动态规划方法？（条件是有最优子结构和重叠子问题，比如有历史依赖性的时候就是不成立的）
    • 找出最优解(Characterize an optimal solution)；
    • 递归地定义最优解的值(Recursively define the optimal values)；
    • 用一定的顺序去计算最优解的值，通常采用自底向上的方法(Compute the values in some order)；
    • 利用计算出的信息构造一个最优解(Reconstruct the solving strategy)；
  • 两种方法：
    • 第一种方法称为带备忘的自顶向下法（top-down with memoization）。此方法仍按自然的递归形式编写过程，但过程会保存每个子问题的解（通常保存在一个数组或散列表中）。当需要一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的值，从而节省了计算时间；否则，按通常方式计算这个子问题。我们称这个递归过程是带备忘的（memoized），因为它“记住”了之前已经计算出的结果。
    • 第二种方法称为自底向上法（bottom-up method）。这种方法一般需要恰当定义子问题“规模”的概念，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因而我们可以将子问题按规模排序，按由小至大的顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解它（也是第一次遇到它）时，它的所有前提子问题都已求解完成。
    • 两种方法得到的算法具有相同的渐近运行时间，仅有的差异是在某些特殊情况下，自顶向下方法并未真正递归地考察所有可能的子问题。由于没有频繁的递归函数调用的开销，自底向上方法的时间复杂性函数通常具有更小的系数。
  • 核心：（找到最优子结构）在递推过程中避免多次求解同一个子问题，用表记录下来它的结果。

1. Fibonacci

原本的复杂度O(N) -> 递归复杂度O(\(2^N\))，递归有大量重复的运算。

Solution:

  • 方法一：在过程中用表记录计算结果，算过的直接查表；
  • 方法二：不是用递归，直接计算记录下来最近的两个数，自底向上直接进行计算；

2. Ordering Matrix Multiplications（矩阵乘法的顺序）

1. 问题描述：

不同的计算顺序下，矩阵乘法的计算量有很大差别，如何才能找到计算量最小的计算顺序很重要。

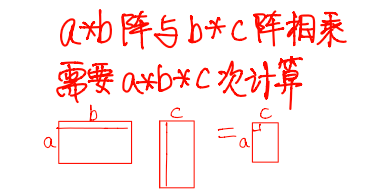
image-20230418164309780

2. 总共的情况：

image-20230418165249915

3. 找出子问题——求\(m_{ij}\)：

理想情况是，\(m_{il}\)和\(m_{(l+1)j}\)已经存在表中，再对\(m_{ij}\)进行计算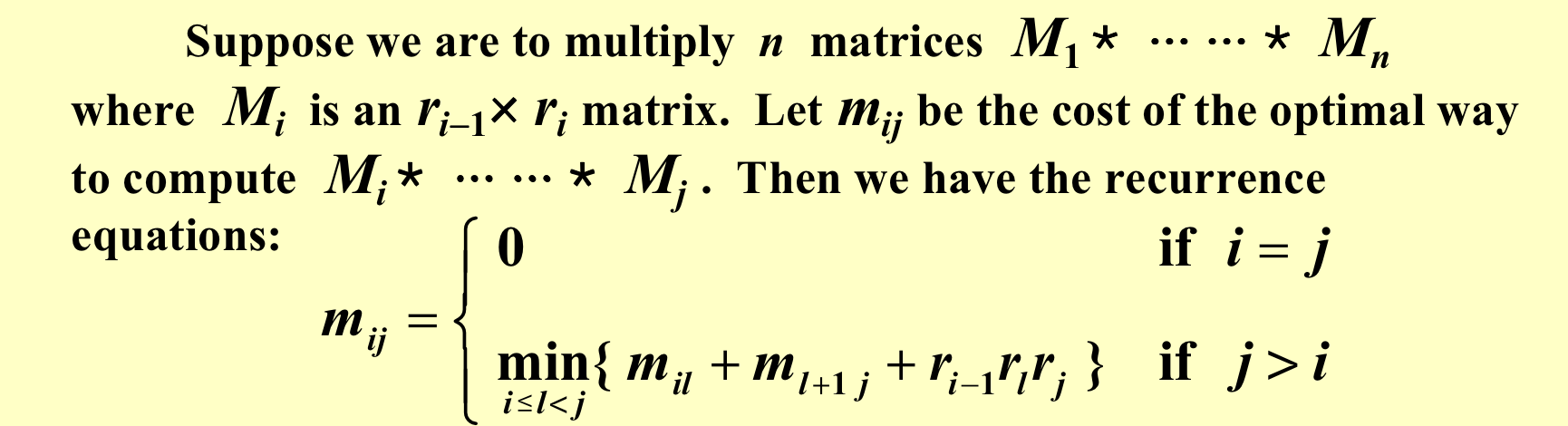image-20230418165639336

也就是说用O(\(N^2\))大小的空间来存储\(m_{ij}\)的结果

4. 具体算法：一层一层地进行计算

image-20230418171331863

5. 最后一步——合并子问题

image-20230418172210085

3. Optimal Banary Search Tree（最优二叉搜索树）

1. 问题描述：

给定词的频率，如何进行二叉搜索树的构建可以使期望代价最小。

总代价：\(d_i\)就是深度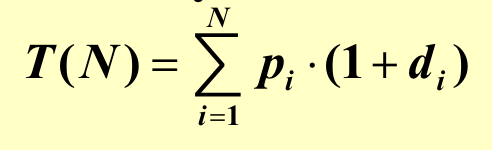image-20230418173004266

2. 具体问题

image-20230418173101089

3. 找出子问题

weight：当前OBST所有节点概率的和

image-20230418175320696

完成最优子结构的寻找拆分后，递归表达式其实跟刚刚的矩阵相乘差不多，那么就一个一个节点去试就好了，也就是l取i～j之间的每一个值。

4. 建立表格并计算结果

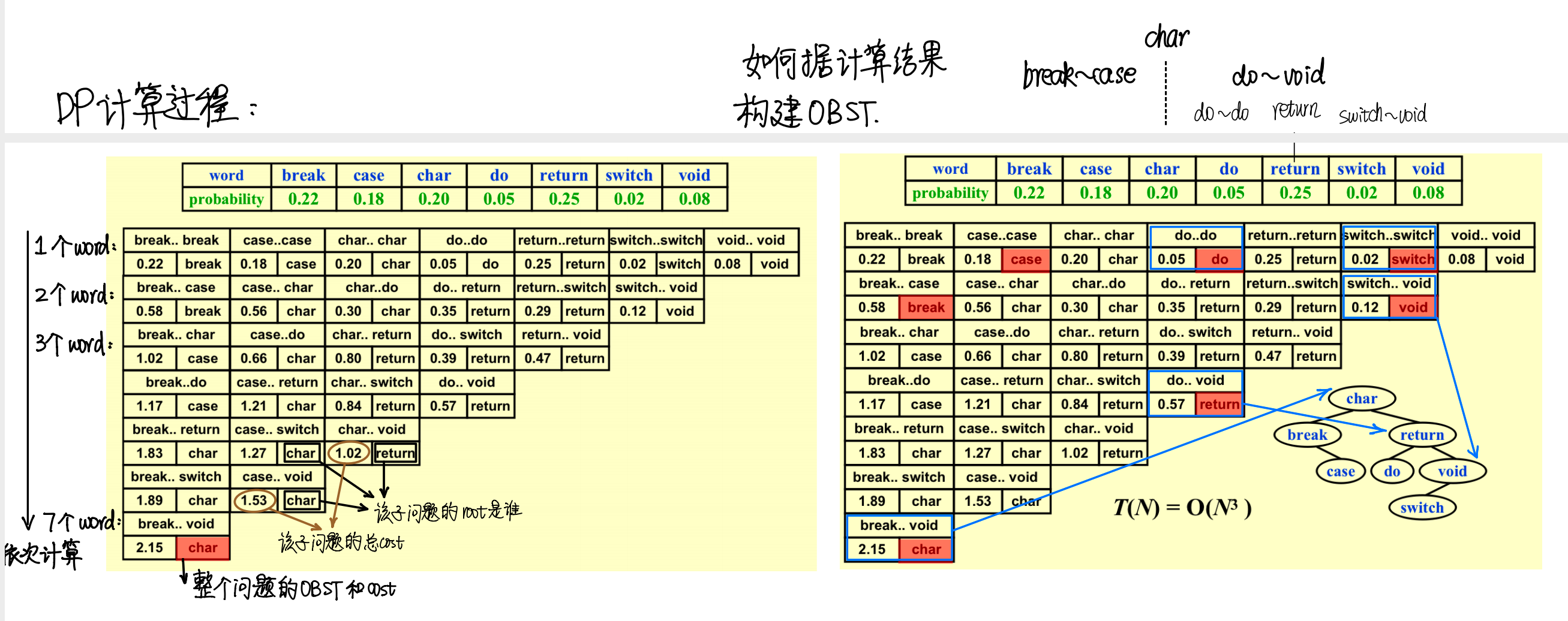
image-20230418180318751

\(T(N) = O(N^3)\)

4. ALL-Pairs Shortest Path（任意两点之间的最短路径）

方法一： 用dijkstra算法，对每个结点使用一次，时间复杂度为\(O(V^3)\)，对于稀疏图比较快。

方法二： k的意思是从i到j只能经过比k小的点，当k不断变大，这个距离可能会变小，\(D^{-1}\)相当于不经过其他的点image-20230418191041129

找到子问题

分为k在i到j的最短路径中和k不在i到j的最短路径中，求两者的较小值，但是如果有负圈的话就不行，这样就不能保证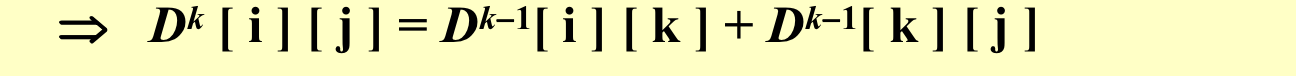image-20230418191901552成立，因为可能两个加起来会有一个圈，此时如果圈是负的，那么就还要把圈减掉，那就不对了；当然有负边是可以的。image-20230418191621514

image-20230418191826856

代码实现

image-20230418193921553

引申思考

如果每条边的权重都是一，怎么进行简化？

矩阵相乘+分治法。直接邻接矩阵相乘，邻接矩阵的n次方（用分治法去求\(logN\)）就代表从这个点经过n条边到另一个点的路径数量，所以比\(N^3\)肯定要小。

5. Product Assembly（产品装配线问题）

问题概述

一些零件需要被装配成一辆车，有两条生产线，零件可以在两条生产线之间来回切换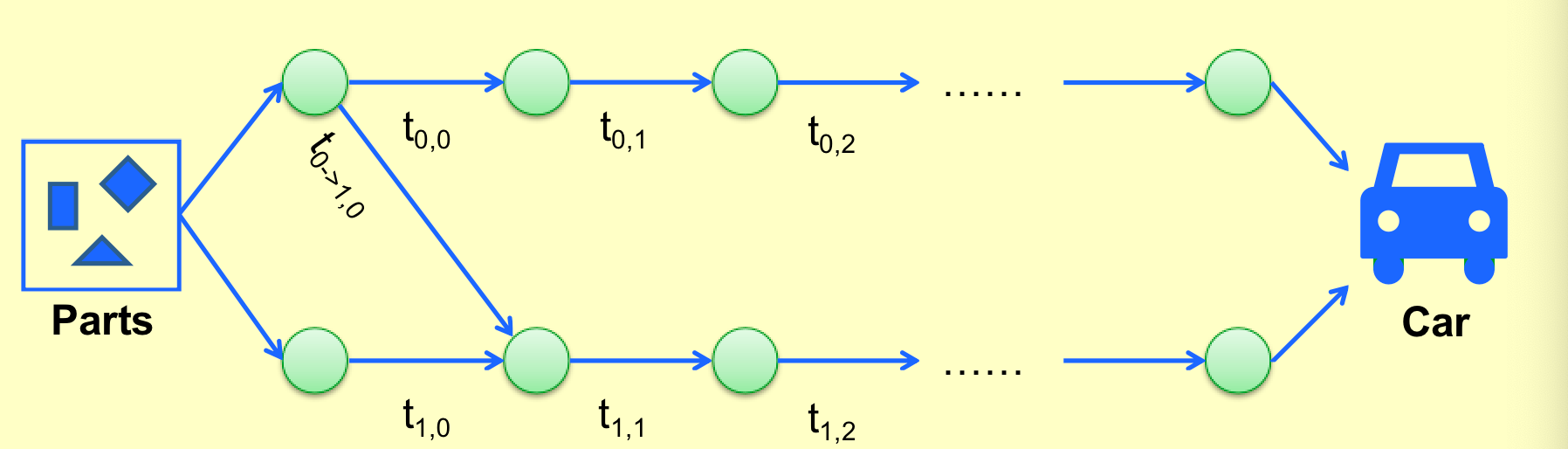image-20230418194503922

最基本的方法需要\(O(2^N)\)时间和\(O(N)\)空间

定义子问题

从0～N的optimal solution一定对于中途的每一个工序来说都是optimal的，对过程中任意的stage，要么从line0来，要么从line1来，到达stage的optimal path由到达stage-1的optimal path来，这就是递推关系。

具体代码

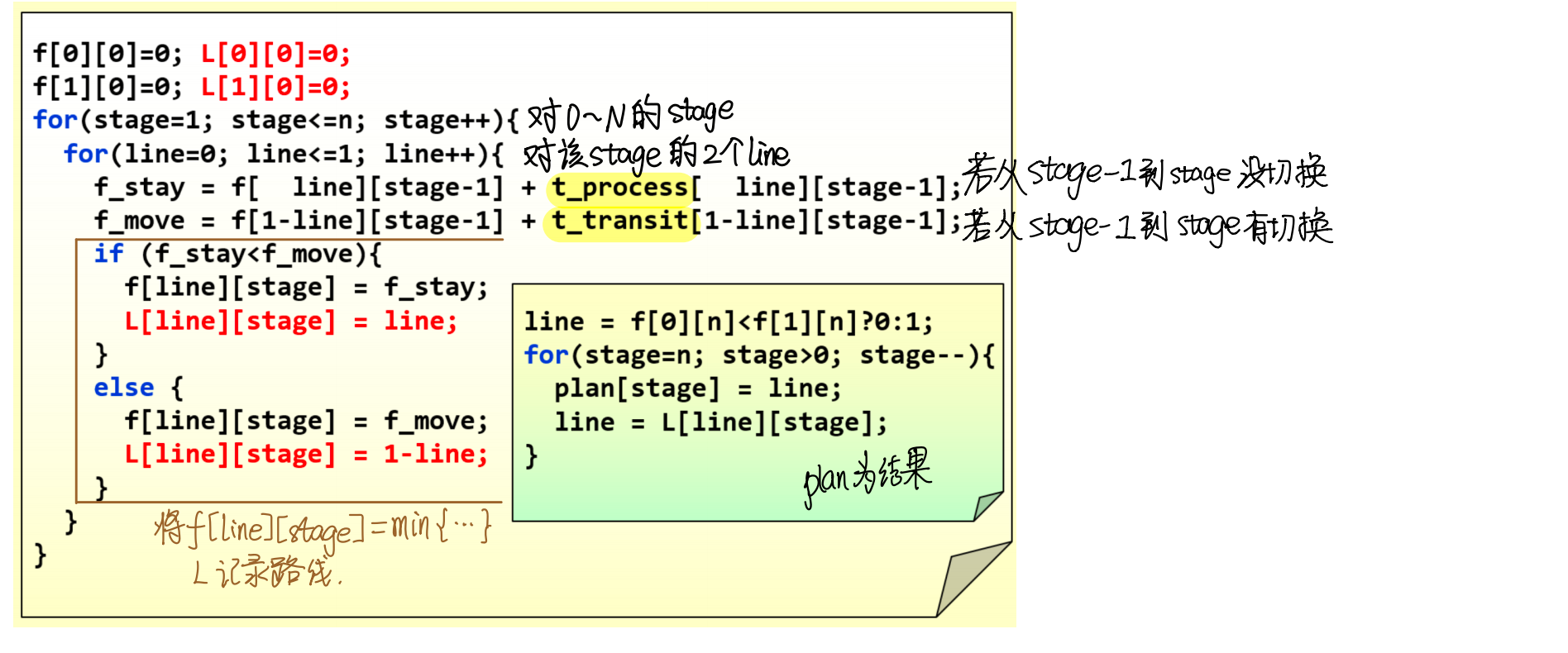
image-20230418195435878

只需要\(O(N)\)的时间和\(O(N)\)的空间

参考资料

  1. ADS08ppt
  2. ADSNotes_Algorithms.pdf(from Carton)
  3. 智云课堂: 2023yds

评论

本文总阅读量次