1.AVL Tree&Splay Tree
约 1264 个字 14 张图片 预计阅读时间 4 分钟
AVL Tree¶
1. balance factor(BF)¶
Order property:左边小,右边大;
Structure property:|BF|<= 1;
与堆相反, 应该先满足Order property;
2. 定义¶
平衡二叉搜索树:balanced binary search tree(BBST) = AVL tree。
高度的定义:空节点的高是1,叶节点高为0,否则就是儿子中高的最大值+1。

3. 为什么要AVL Tree¶
推论
定理:有n个结点的平衡二叉树,是一个斐波那契数列,最后求得高度不高于\(O(logn)\).
证明:先证明引理->任何高度为h的平衡二叉树的结点数小于\(c^h\)(其中\(c\)是一个常数)
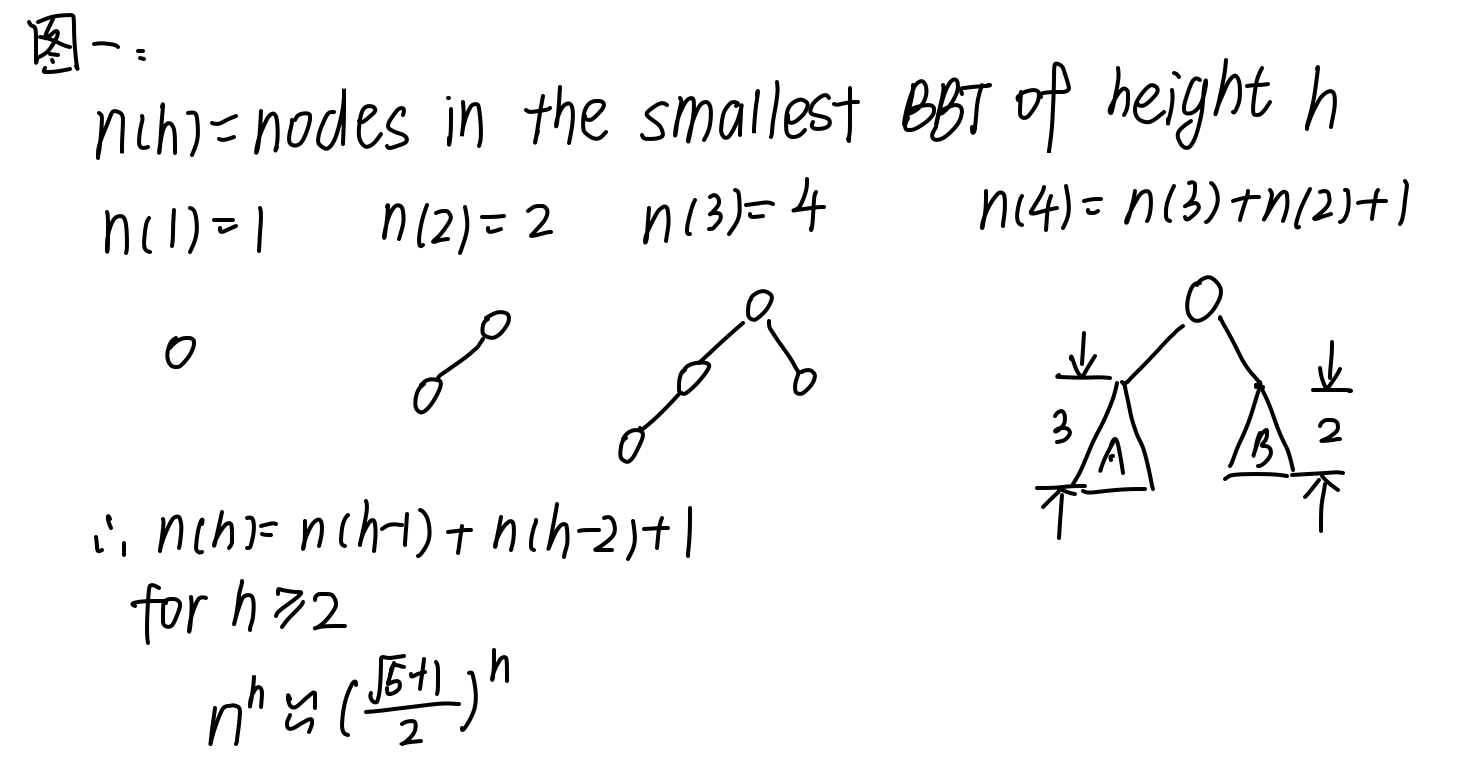
而这个性质很容易维护,所以就有了AVL Tree。

4. Rotation 操作¶
4.1 right rotation¶
- 只需要改三个指针,所以时间是O(1);
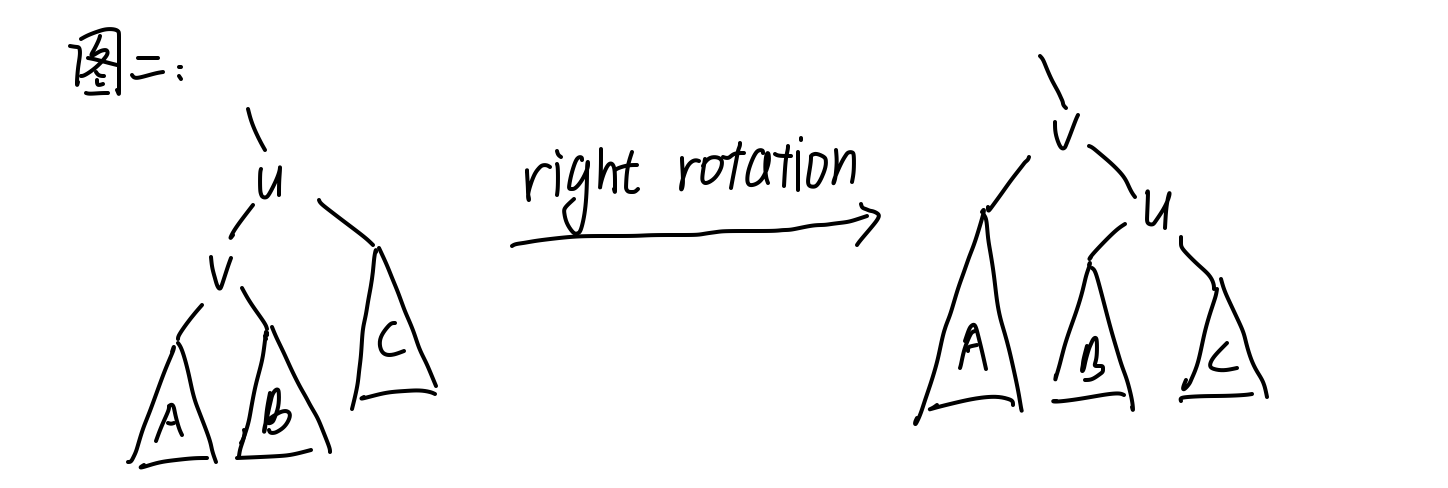
- 旋转能够维持BST性质;
- 旋转会改变高度差,即会改变BF;
4.2 left rotation¶
5. Insertion¶
5.1 Left case¶
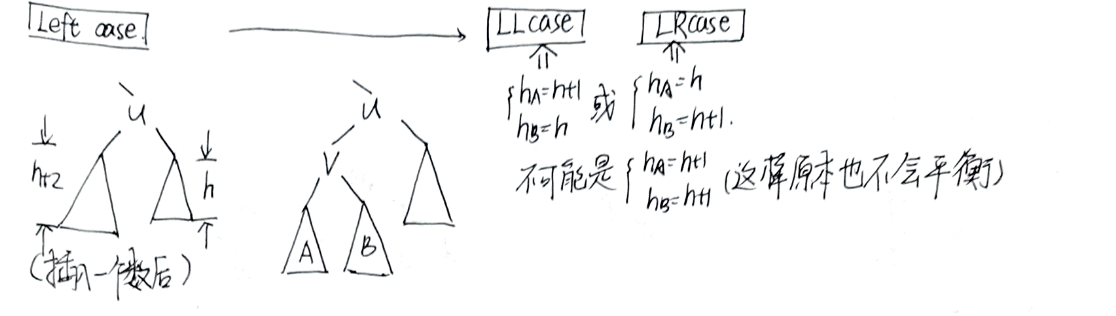
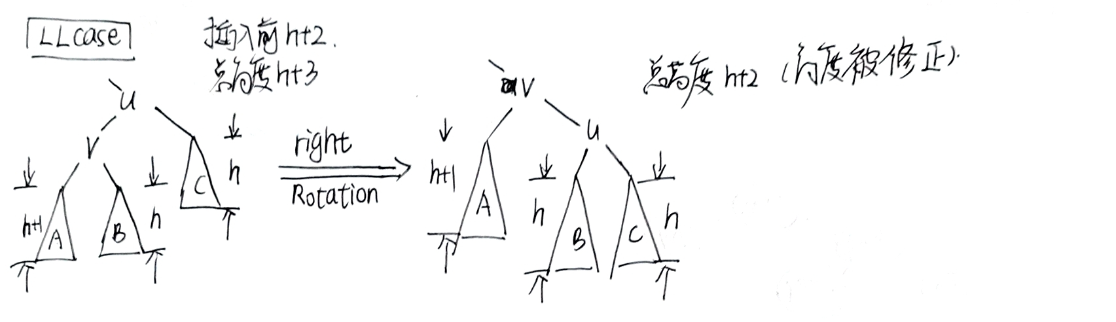
LLcase(LLRotation)¶
LRcase(LRRotation)¶
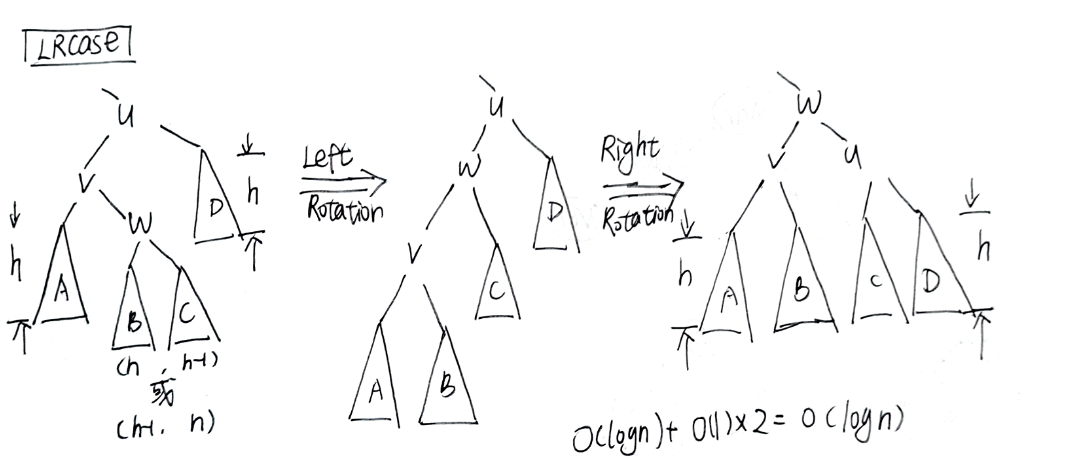
5.2 Right case¶
5.3 总结¶
只要修正了最下面那个节点,其他因他而起的不平衡节点都会被修正。
插入引起的不平衡最多两次旋转就能修正。
case的划分就是破坏者和被破坏者的关系,找的是被破坏者以下的三层,下面的不用看。
不管是这四种的什么情况,最后都要变成中间一个两边各一个的情况,剩下的四块按顺序搬运过去。

6. Deletion¶
- 步骤:
- 像BST一样delete;
- 恢复平衡;
-
在结构上必定会删除一个leaf;
-
删除只会让一个点变得不平衡,但是修复不平衡时候,旋转一次可能会把不平衡向上传,一直传到根结点为止。所以最多旋转\(O(logn)\)次才能修复,所以最终时间还是为\(O(logn) + O(logn)* O(1) = O(logn)\)。
7. 总结¶
综上所述,AVL树的高度是\(logn\)级别的,并且维持树平衡的代价也是\(logn\)级别的。
Splay Trees¶
1. 核心思想¶
- 不要求每一步都做得很好,但是平均下来时间复杂性要小于等于\(O(logn)\)。
- 要找一个对象(其实是任何一个动作,包括插入),那就顺便把这个对象翻到树根(这样下次查找到他的概率就会大一点)。
2. 不好的情况¶
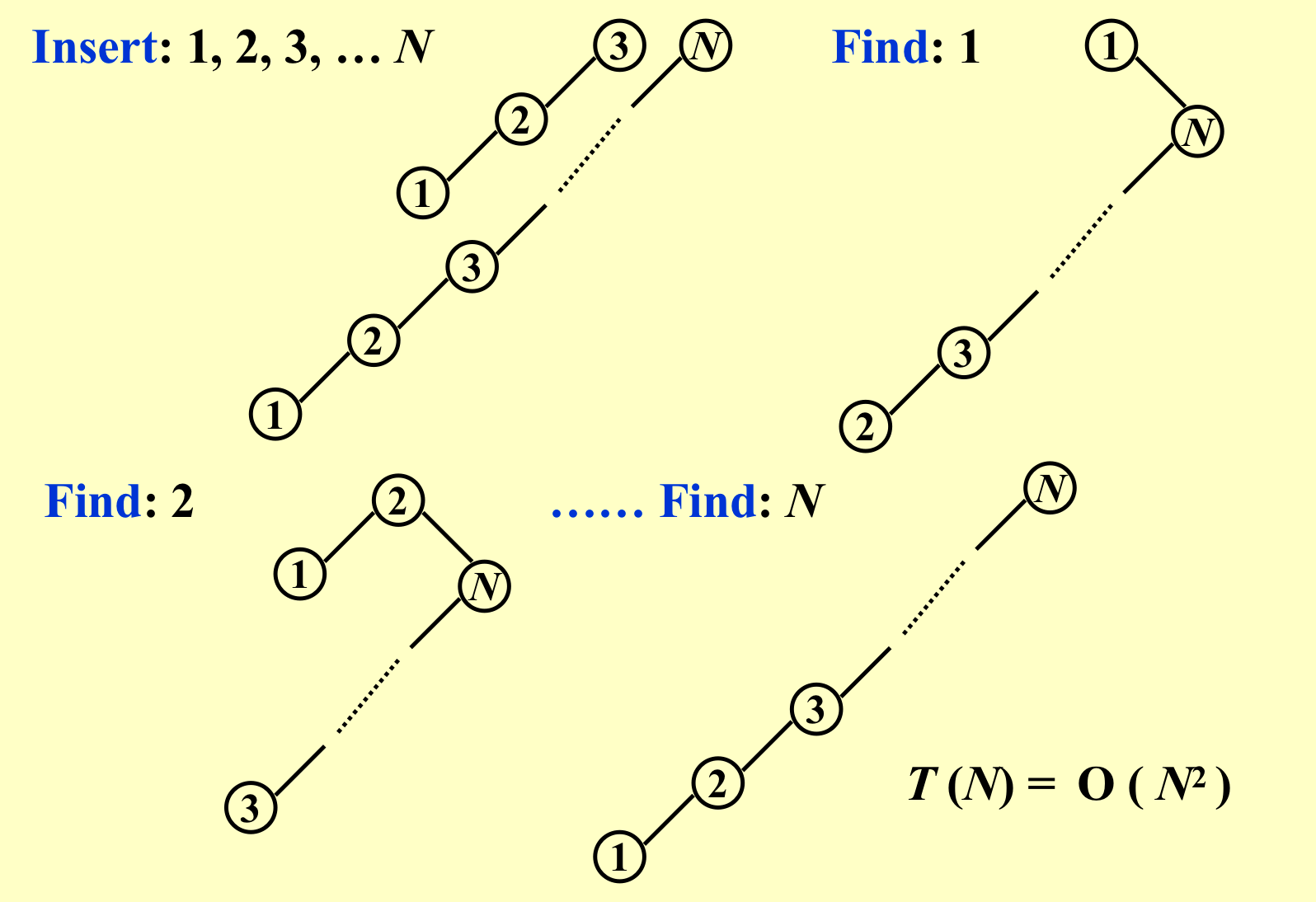
3. 优化¶
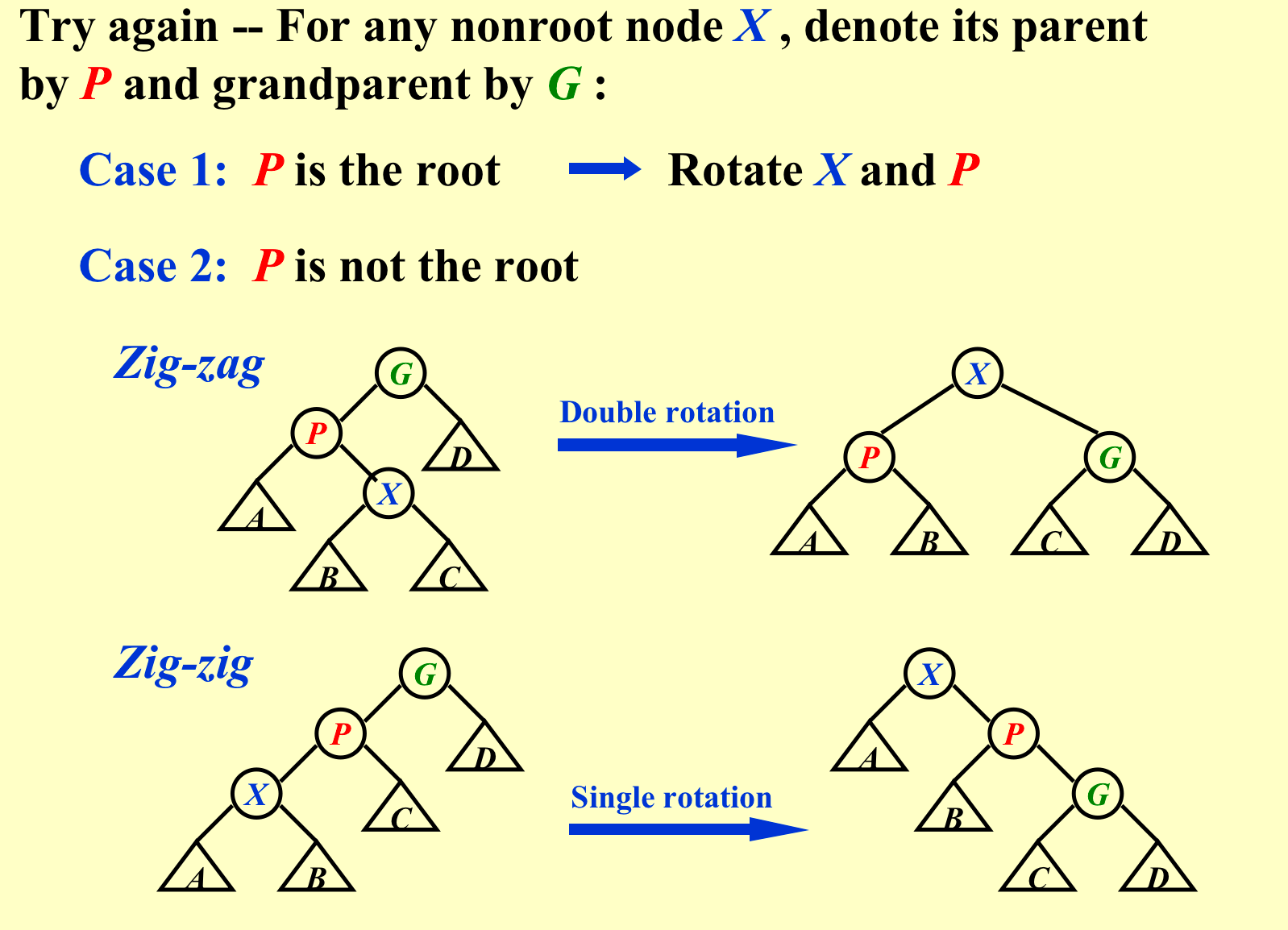
变换过程中不一定两边高度差不超过1;
4. 删除¶
- 找到要删除的节点X,将它旋转到跟节点上(Find X);
- 把跟节点删除,产生左右两颗子树(Remove X);
- 在左子树上找到最大的节点并将他旋转到根节点上(FindMax( \(T_L\) ));
- 把右子树接到左子树根的右边(根已经是最大的了,不可能有右孩子);
Amortized Analysis(均摊代价分析)¶
点此跳转
定义¶
- Amortized Bound:任意多次操作的时间复杂性上界;
- Average-case Bound:无限多次操作的时间复杂性上界;
解决方法¶
Aggregate analysis(累计分析)¶
以push,pop,multipop为例,n次操作,最多只有n个元素,所以mutipop最多也是\(O(n-1)\),所以总时间复杂性就是\(O(n)\),所以每个的时间就是\(O(1)\)。
Accounting method(记账方法)¶
总的时间等于push的两倍
摊还时间 = 实际时间 + credit
在假设了一个要证明的均摊复杂度后,对实际的每步操作,如果实际消耗比均摊消耗低,那么把差值作为“余额”存起来,余额可以为其他操作中实际消耗比均摊消耗高出的那部分“付款”。最后只需要证明每一步的均摊消耗之和大于等于实际消耗之和。(from JerryG 20级)
| 操作 | 实际代价 | 摊还代价 |
|---|---|---|
| push | 1 | 2 |
| pop | 1 | 0 |
| multipop | min(k,s) | 0 |
总和方法对所有的操作一视同仁,而记账算法不同,每个操作的credit不尽相同。
我们可以把摊还代价设置成这样是因为pop次数之和肯定不会超过push的次数,因此可以保证任何情况下信用值不是负数,而此时摊还代价总和的上界为2n所以平均的摊还代价是O(1)。(from 小角龙)
Potential method(势能法)¶
点此跳转
核心:让消耗大的那一步操作势能大大的降!

对账目分析法的一种形式上的改进。定义数据结构自身状态的“势能”函数, 每次操作可能改变自身的势能,势能的改变跟跟余额的改变(每一步均摊和实际的差值)有密切关系,或者说相等。势能最开始取最小值,每一步中,势能增加量等于均摊消耗比实际消耗多出的部分。定义完势能函数后,均摊复杂度一定是大于势能函数每一步的最大可能的增长值的,所以要定义增长尽量缓慢的势能函数,同时又能表现实际操作和均摊操作的关系(这里不太容易说清楚)。势能函数的最大值往往决定了均摊分析的结果。(JerryG 20级)

分析伸展树¶
点此跳转
-
每个结点的势能计算。
-
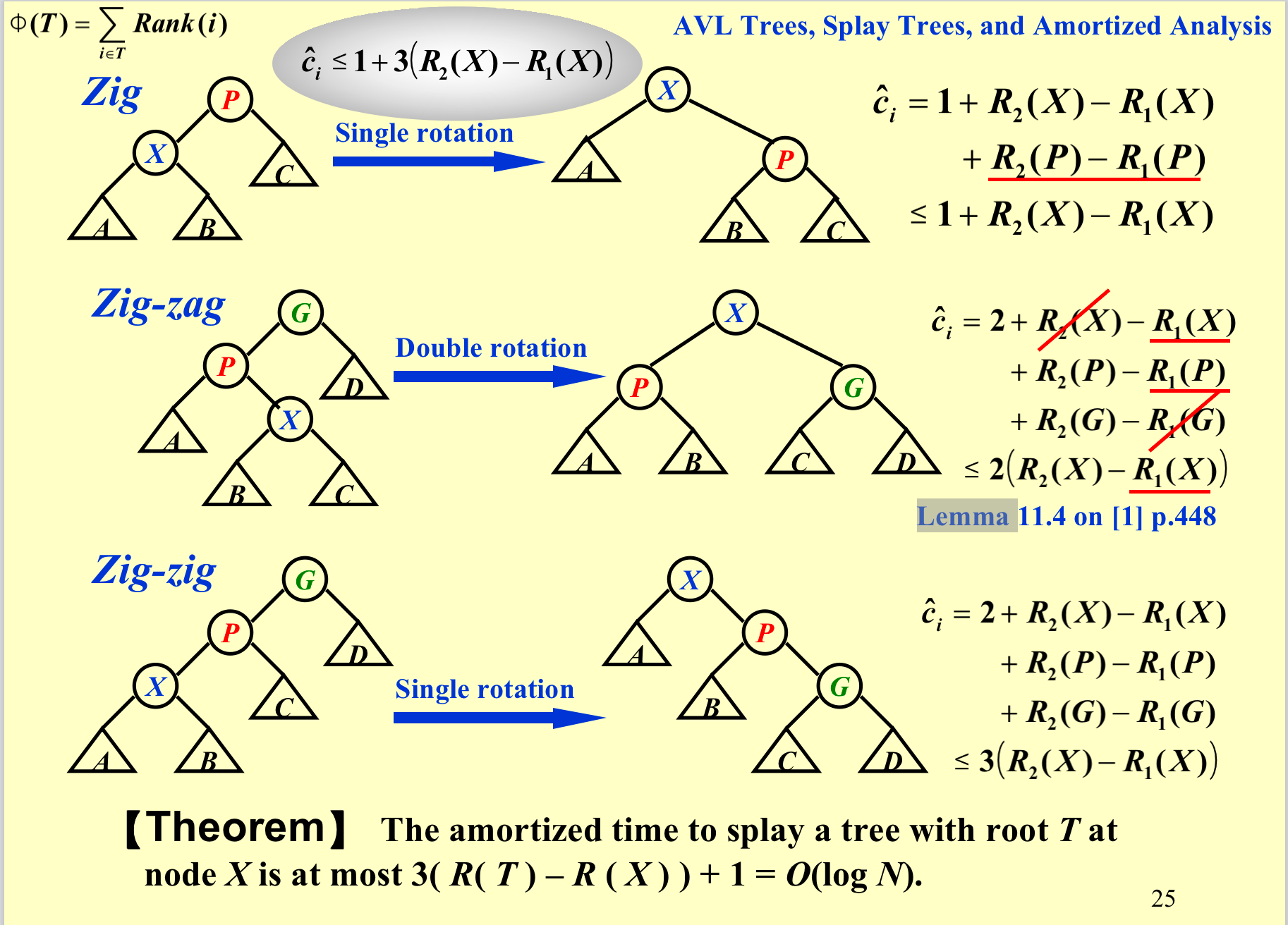
Quote
- ADS01AVL_Stu.ppt
- 小角龙(18)复习笔记.pdf
- JerryG(20)复习笔记.pdf
- 智云课堂:2023myc,2022hqm,2022yds
评论
本文总阅读量次