lec1-6
约 746 个字 5 行代码 18 张图片 预计阅读时间 3 分钟
Lec 1¶
1. algorithm¶

程序使用编程语言写的,不一定是有限的(比如操作系统);
2. Analyze¶
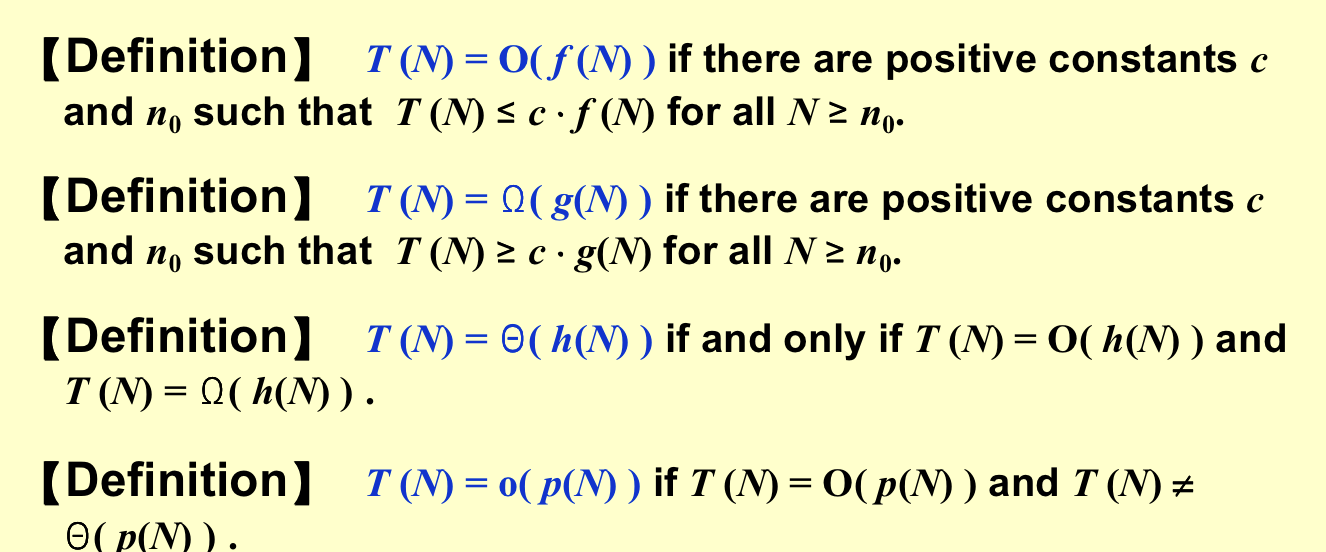

O可能包含等于的情况,而o是严格小于 nlogn比n快 对数平方比对数快
Lec 2¶
1. 求最大子序列¶
Divide and Conquer¶
求两边求中间,递归终点如下:
if(left == right)
if(seq[left] > 0)
return seq[left];
else
return 0;
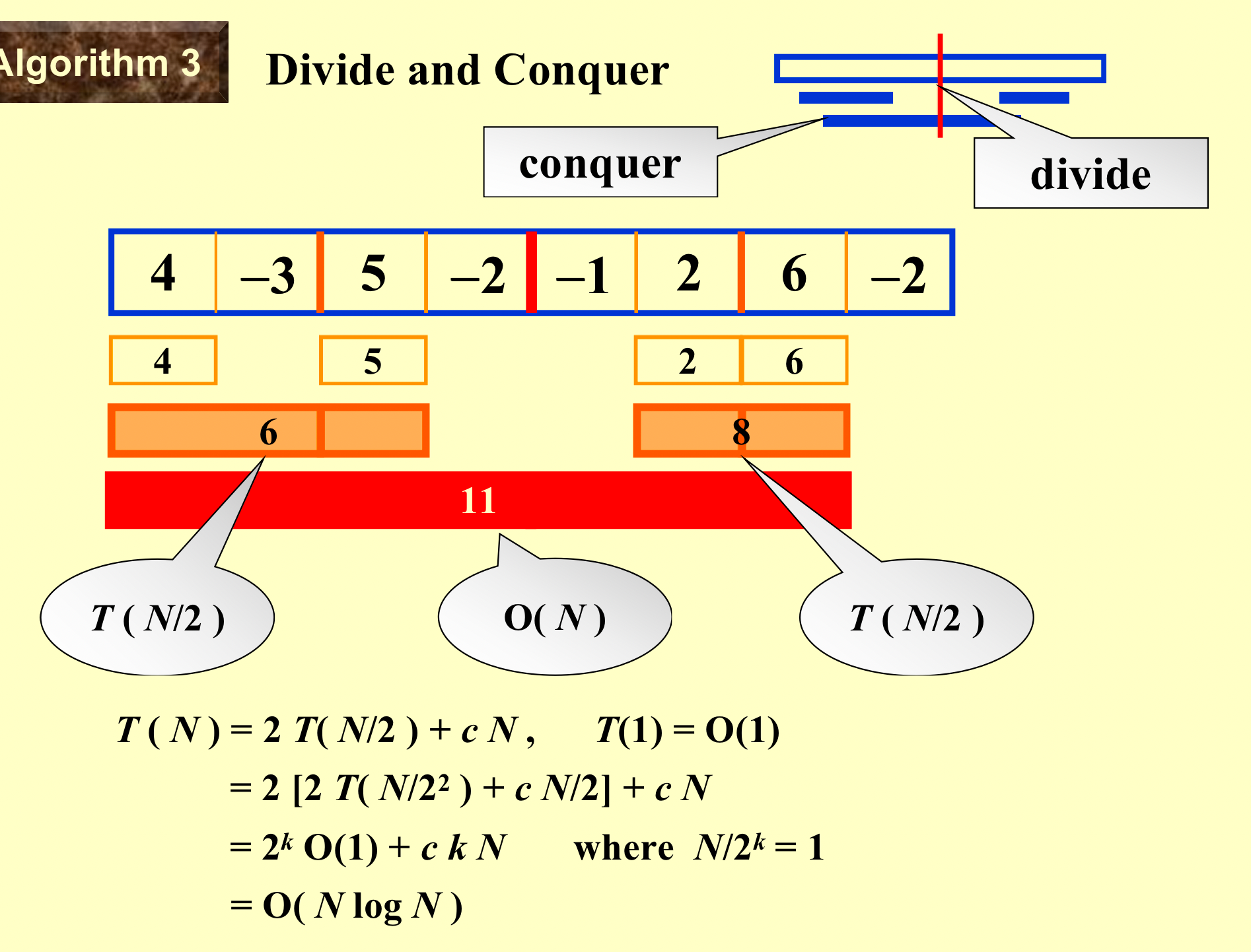

On-line ALgorithm¶

2. Lists, Stacks and Queues¶
2.1 ADT¶
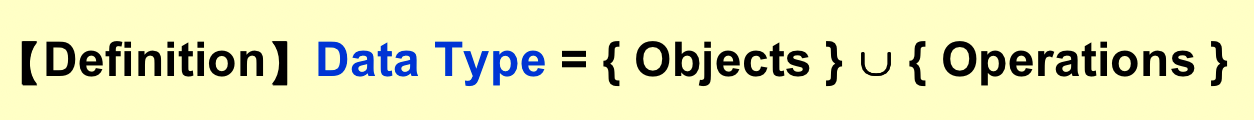
linked lists¶
-
需要熟悉各种操作,插入、删除、反转;
-
Insertion: >temp->next = node->next; node->next = temp;
-
Deletion: >pre->next = node->next; free(node);
-
有无头节点;
Lec 3¶
Cursor Implementation of Linked Lists (no pointer)¶
The Stack¶
操作较为简单,不再赘述,谈到多项式的处理,复习逆波兰表达式,又谈到函数调用。

The Queue ADT¶
队尾插入,队首删除; front 和 rear 指向头和尾会导致空和满是一样的,无法区分;
- 本质上是信息不够,加变量;
- 少一个元素(这种情况下可以rear指向最后一个元素后的一个位置);
Lec 4¶
Trees¶
定义¶
- degree of a node ::= number of subtrees of the node. For example, degree(A) = 3, degree(F) = 0.
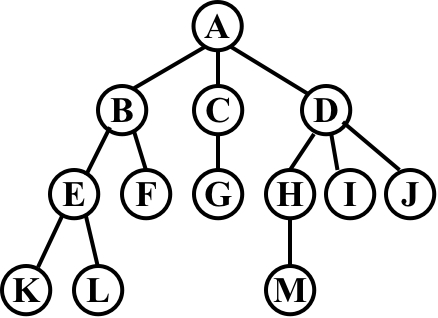
- degree of a tree ::= max of the node degree. For example, degree of this tree = 3.
- siblings ::= children of the same parent.
- length of path ::= number of edges on the path.
- depth of ni ::= length of the unique path from the root to ni. Depth(root) = 0.
- height of ni ::= length of the longest path from ni to a leaf. Height(leaf) = 0, and height(D) = 2.
- height (depth) of a tree ::= height(root) = depth(deepest leaf).
Binary Trees¶
【Definition】A binary tree is a tree in which no node can have more than two children.
- 利用队列来实现中序遍历;
- 利用循环来实现中序遍历;
- 左边走到底,边走边压栈;
- tree赋值栈顶,pop栈顶元素;
- 判断是否为空,如果空,则break;
- 如果不空,输出;
- 向右走;

Threaded Binary Trees¶
有了线索很方便,如果不是线索,就向右走到底,是线索就按线索来;
加一个头节点来指向中序的起点和终点;

Lec 5¶
后序遍历第一个点¶
左边走到底,往右走一步,再左边走到底,直到两边都没有了;
完全二叉树¶
除了最后一行都是满的,最后一行不满的也是在后面;
二叉树的性质¶
For any nonempty binary tree, n0 = n2 + 1 where n0 is the number of leaf nodes and n2 the number of nodes of degree 2.
证明:每个结点往上看,边的条数:n0 + n1 + n2 - 1;每个节点往下看,边的条数:n1 + 2n2;
//三叉树四叉树也有类似的结论;
Binary Search Trees¶
定义¶

查找树的中序遍历一定从小到大;
操作¶
1. Find¶


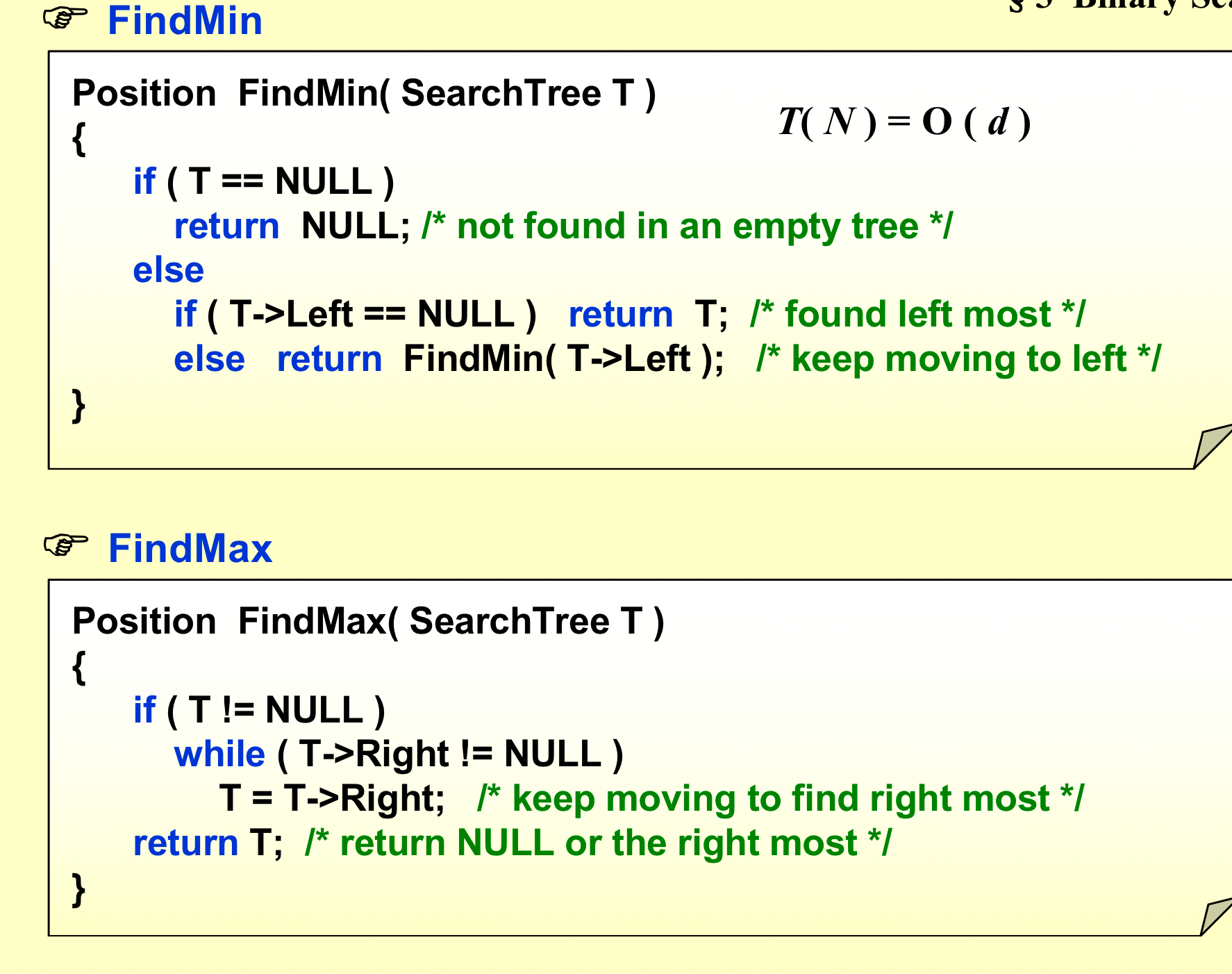
2. FindMin & FindMax¶
3. Insert¶

4. Delete¶
importent!!

lazy_deletion也可以,用空间换时间。不真的删除,只是做个标记;
Lec 6¶
Heaps¶
对于堆的操作,先保证其结构,在保证其是堆;
insertion¶
先放进最后,然后逐步往上比较;
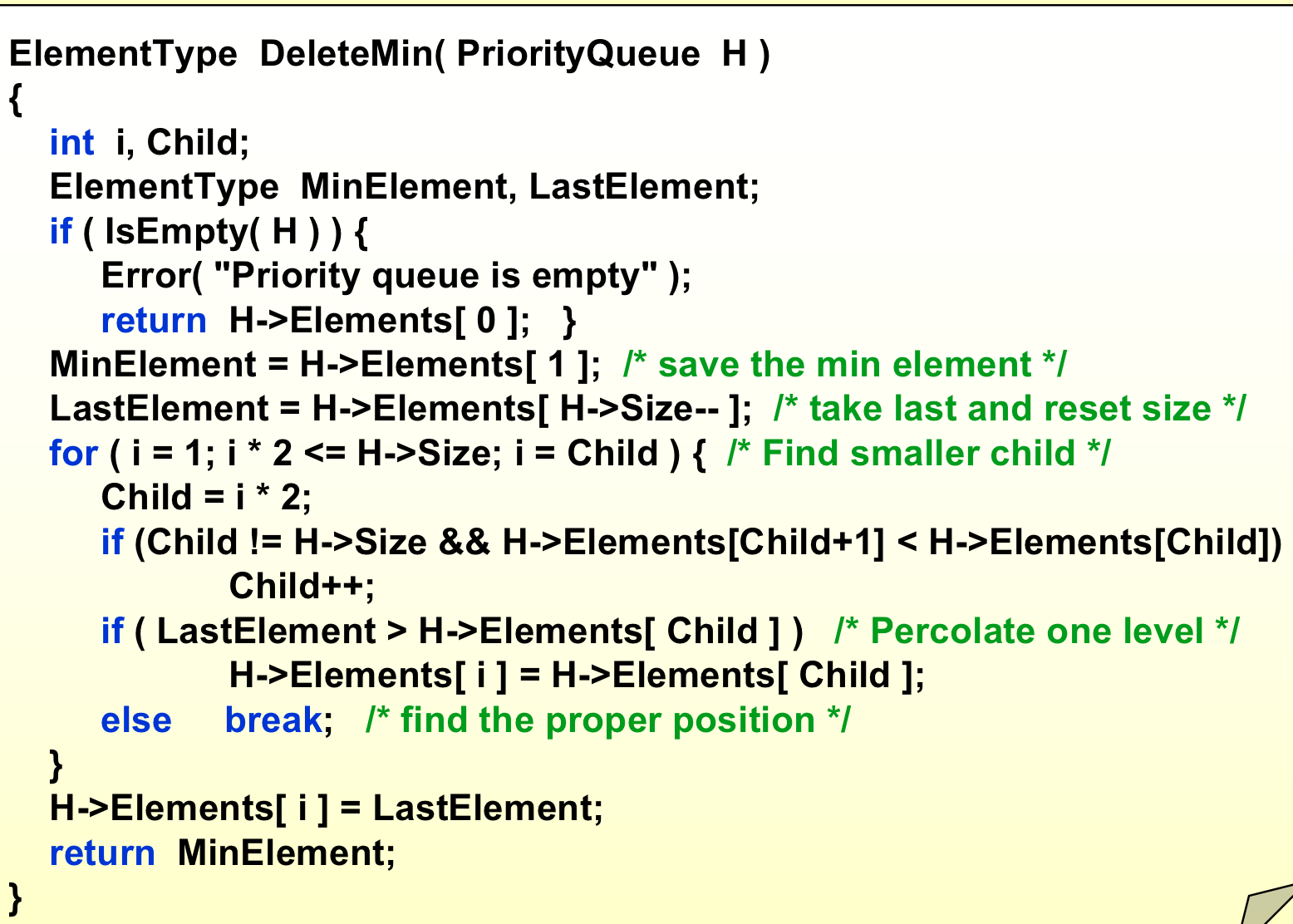
DeleteMin¶
把最后的一个放进根,然后跟insertion一样进行比较;
BuildHeap¶
- 先把所有放进数组中,然后最后一排结点开始,自下而上全部转化成堆;
- 当成一个一个插入,速度比方法一慢;
d-Heaps¶
All nodes have d children;
本文总阅读量次