lec10

约 1012 个字 9 张图片 预计阅读时间 3 分钟

Depth-First Search(DFS)

1. 用处

• 双连通子图（任意两个点都有两条路径）
• 欧拉回路（一笔画，把所有边走一遍）

2. 算法实现

• 深度优先算法实现（访问顺序看for是如何访问的）；

• 无向图是连通的，当且仅当从任意结点开始的深度优先搜索访问到每一个结点；

  • 如果连通：

  • 如果不连通（可以用来求连通分支的个数）：

3. 双连通子图的一些定义

• 如果一个连通的无向图中的任一顶点删除之后，剩下的图仍然连通，那么这样的无向连接图就称为双连通的（biconnected）。G is a biconnected graph if G is connected and has no articulation points.
• v is an articulation point if G’ = DeleteVertex( G, v ) has at least 2 connected components. 即，如果一个图不是双连通的，那么将其删除后图将不再连通的那些顶点叫做割点（articulation point）
• A biconnected component is a maximal biconnected subgraph.

Finding the biconnected components of a connected undirected G

• 先随便找一个点使用DFS；
• back edge连接的一定是祖先后裔的关系；
• number值按照深度遍历的顺序；
• low值就是消息所能传到的最高级别（实线不算）；

• 1.如果根结点有两个以上的儿子，一定是关节点（因为根的两边不会有连线）；
• 2.至少有一个儿子通不了天就是关节点；

• 更新low值相当于后序遍历，因为儿子要先更新；

双连通子图程序

• 第一趟遍历，先和dfs一样对进行num赋值；

• 第二趟第三趟遍历都是后序遍历，计算low并检验是否割点；

• 一次遍历就实现；

4. 欧拉路径与回路

• 1.判定：

  • 欧拉回路存在当且仅当图是连通的且每个节点的度都是偶数；（An Euler circuit is possible only if the graph is connected and each vertex has an even degree.）
  • 欧拉环路，An Euler tour is possible if there are exactly two vertices having odd degree. One must start at one of the odd-degree vertices.

• 2.算法：

  • 任意一点出发深度遍历（这样一定能回到原点，因为有边出去一定有边回来，因为是偶数的度）；
  • 回到原点后，沿着刚刚遍历出来的环走，一定能够发现一个点有边没走完（如果都走完了，那程序就可以结束了）；
  • 然后刚刚那个没走完的点为原点，重复上述操作；
  • 这样遍历出来了两个环，把两个环并成一个大环，这个大环肯定有点的边没走完；

• 提了一嘴哈密顿通路问题；

图论总结

• 图分成点和边，那么如何表示边的结构：
  • 用矩阵表示，即邻接矩阵；
  • 用链表表示，一般的用邻接表和逆邻接表，有向图十字链表，无向图多重链表；
• 图的核心基础算法：
  • 深度遍历；
  • 宽度遍历；
  • 然后在遍历过程中不断通过一个点更新另外的点；

排序

• 排序分类：
  • 内排序（放在内存里排序）
  • 外排序（把数据放在硬盘里，一部分一部分排序，最后使用归并排序）
• 排序方法：
  • 简单排序
  • 插入排序：假定前面i个已经排好了，插入后一个元素；（最快N，最小N²）
  • 冒泡排序：最大的冒泡到最后；
  • 选择排序：从头到尾看一遍，挑一个最大的，和最后一个交换；
  • 简单排序的特点：
    • 比较+交换；
    • 无法突破N²，对于N个数，平均的逆序为N²，而交换一次只能改变一个逆序；

快速排序

Shell（分组排序）

• 分成若干组，各自排序好后，再分成若干组，逐渐粗放，到最后只分一组，运用插入排序（插入排序越有序越快）；

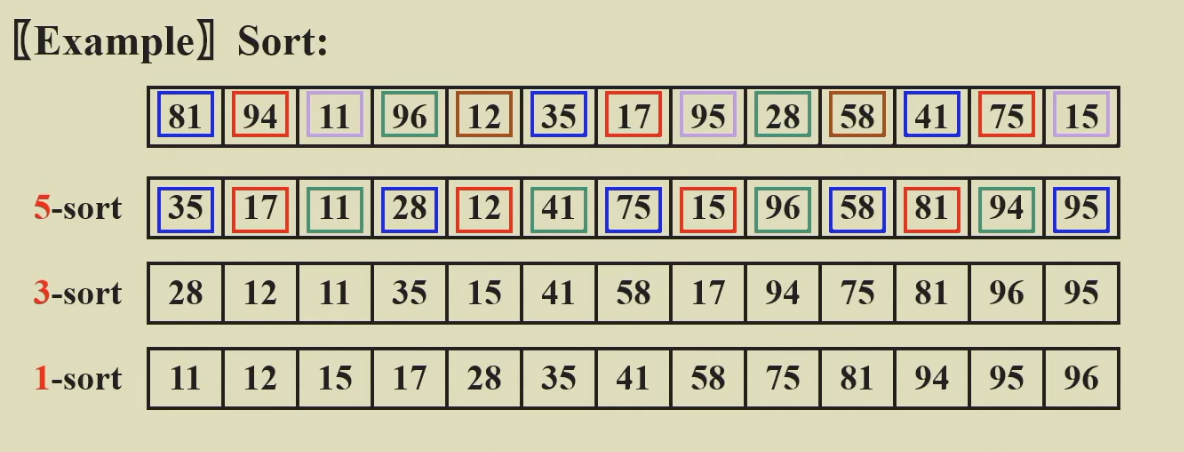
qsort（快速排序）

• 冒泡排序升级版；

堆排序

• 选择排序升级版，因为选择排序是要找到最大的，所以我们就用堆来找最大的；

基数排序

本文总阅读量次