lec13-14
约 665 个字 27 张图片 预计阅读时间 2 分钟
0. 复习排序¶
- 算法的特点
- 给你一个序列，告诉你经过两轮排序的结果，问用什么方法；
- 各种算法的时间复杂性
- 简单排序
- 快速排序（基数排序跟位数有关系）
- 各种算法的空间复杂性（指要用多少额外的空间
- 快速排序用到递归（O（logN））；
- 算法排序的稳定性问题
- 保证相同的数值，本来在前面之后还是在前面，那么就是稳定的；
- 一般会跨越交换的就是不稳定的；
1. HASHING¶
本质上是空间换时间；
1.1 General Idea¶
管理与操作字典：插入单词，删除单词，查找单词（最主要）；
Hash Tables¶
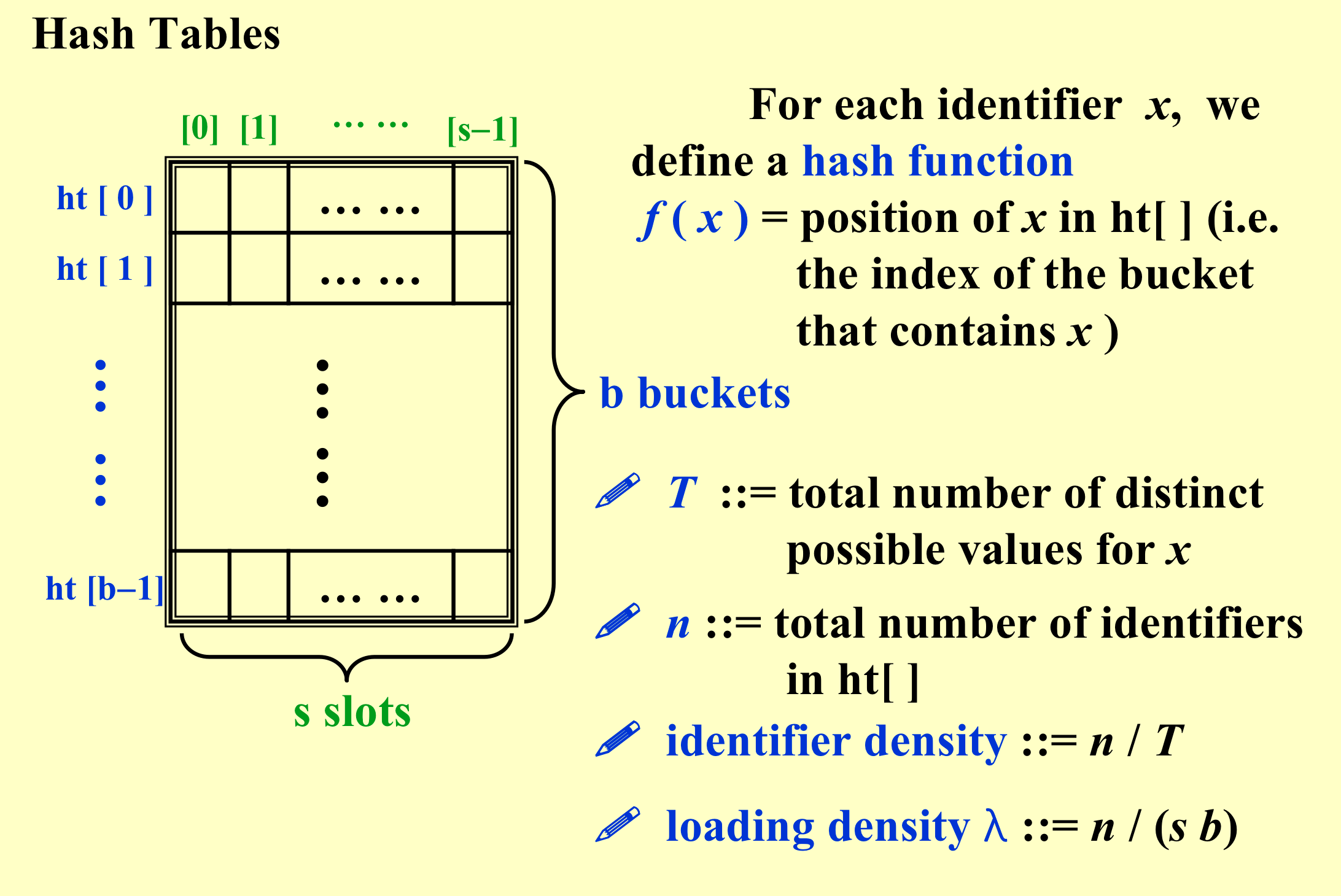
目标：设计一个好的哈希函数；设计一个好的解决冲突算法；
1.2 Hash Function¶
特点¶
-
（好算）f ( x ) must be easy to compute and minimizes the number of collisions.
-
（没有偏见，均匀映射）f ( x ) should be unbiased. That is, for any x and any i, we have that Probability( f ( x ) = i ) = 1 / b. Such kind of a hash function is called a uniform hash function.
哈希函数¶
- 求余法；（用素数比较好）
- 平方取中法（平方，取中间的数字为哈希值）；
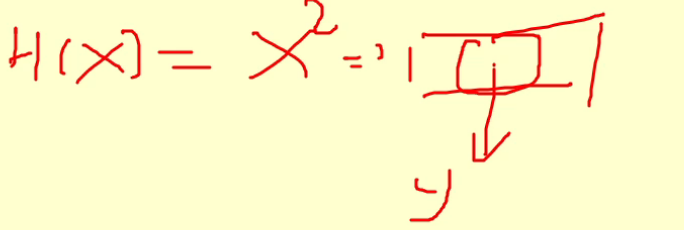
- 折叠法（分成n块，再加起来，就是最后的哈希值）；
- 数字分析法；
例子（整数、字符串¶
把x27改成向左移动五位；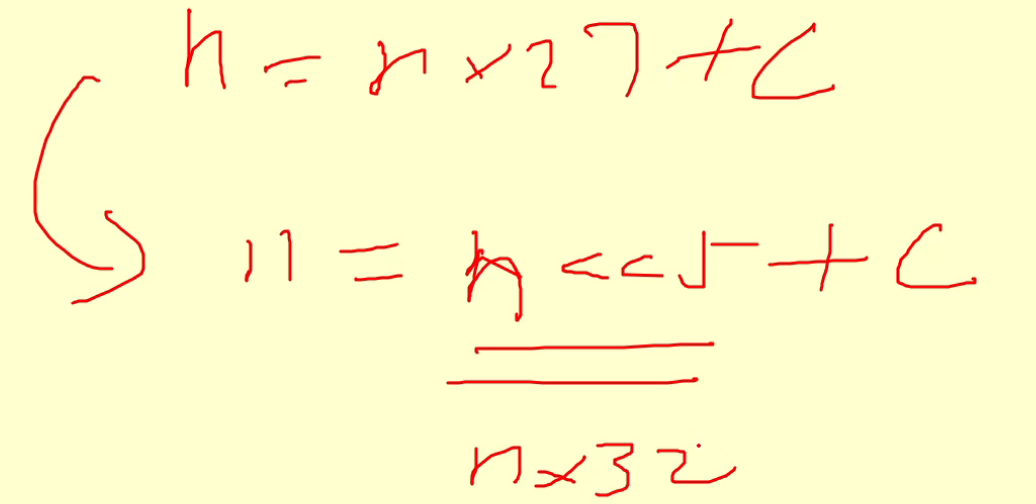
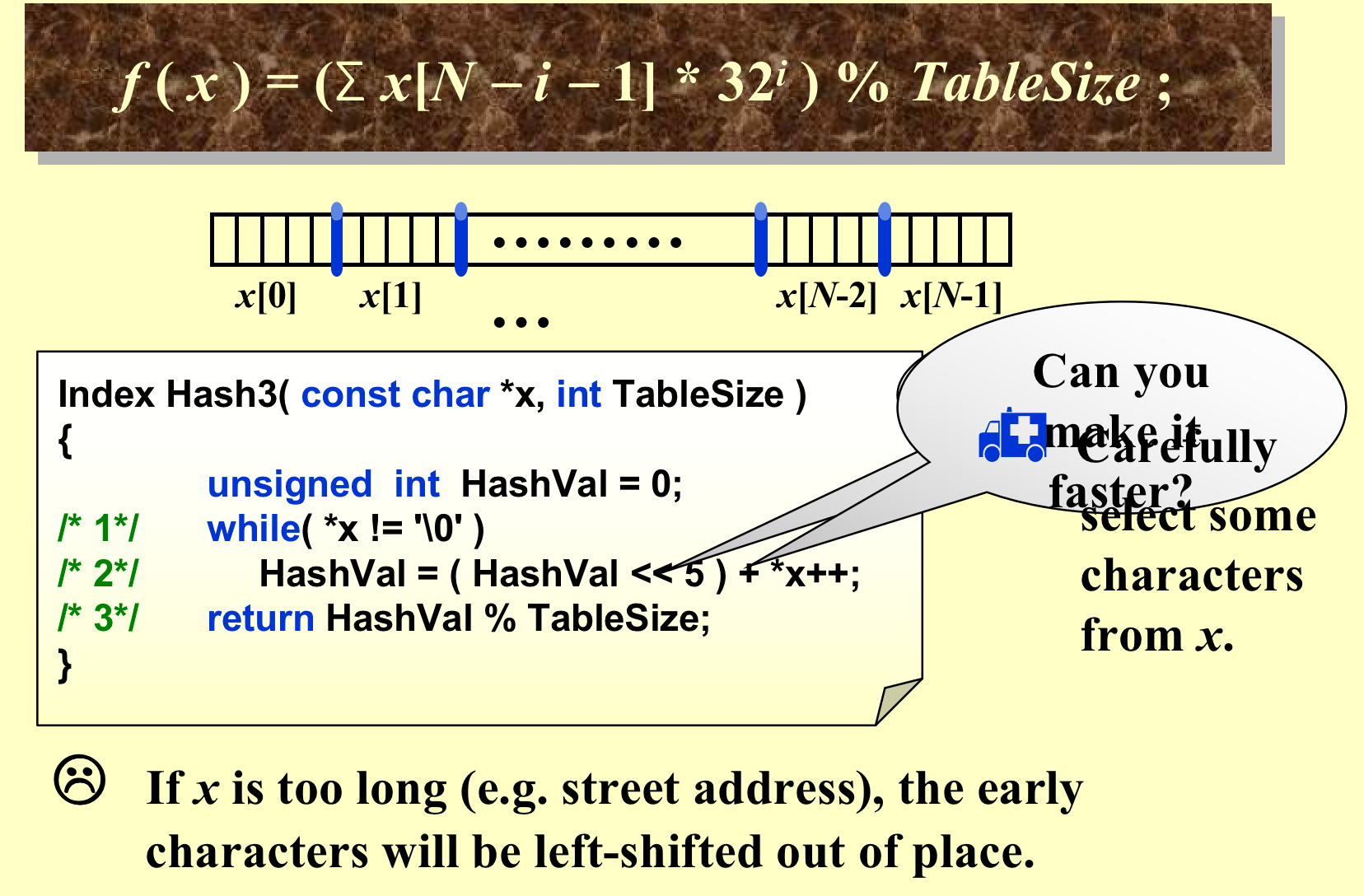
1.3 Separate Chaining（解决冲突）¶
方法¶
- Separate Chaining，一层一层往上累加；
- 开放地址法之线性探测，有冲突就会往后找；
- 公共溢出区法，冲突的全部记在一起；
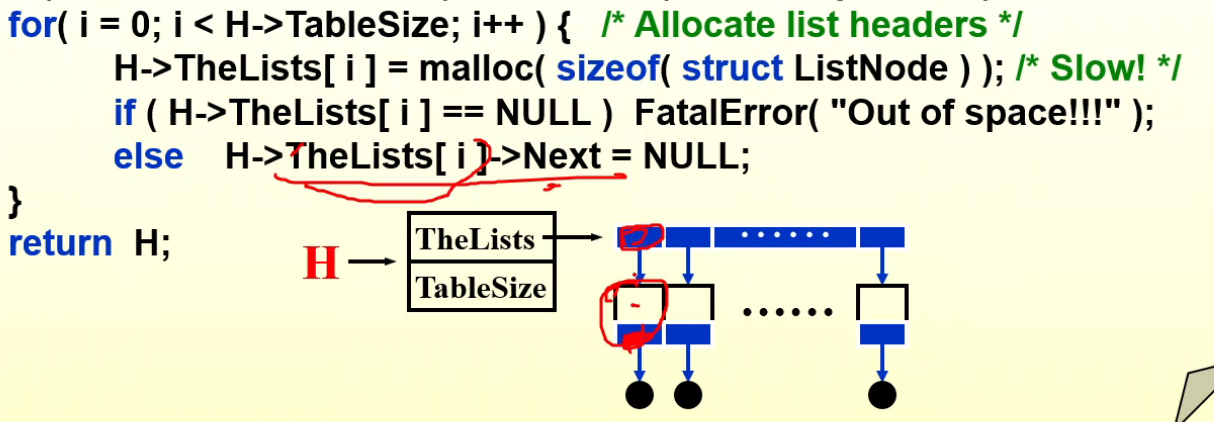
创建代码¶
-
首先判断，如果比较小直接插入排序就好了，不需要哈希；
-
申请空间产生一个哈希表；
-
比table size大一点的素数作为table size；
- 产生指针数组；
- for循环，设置空头结点；
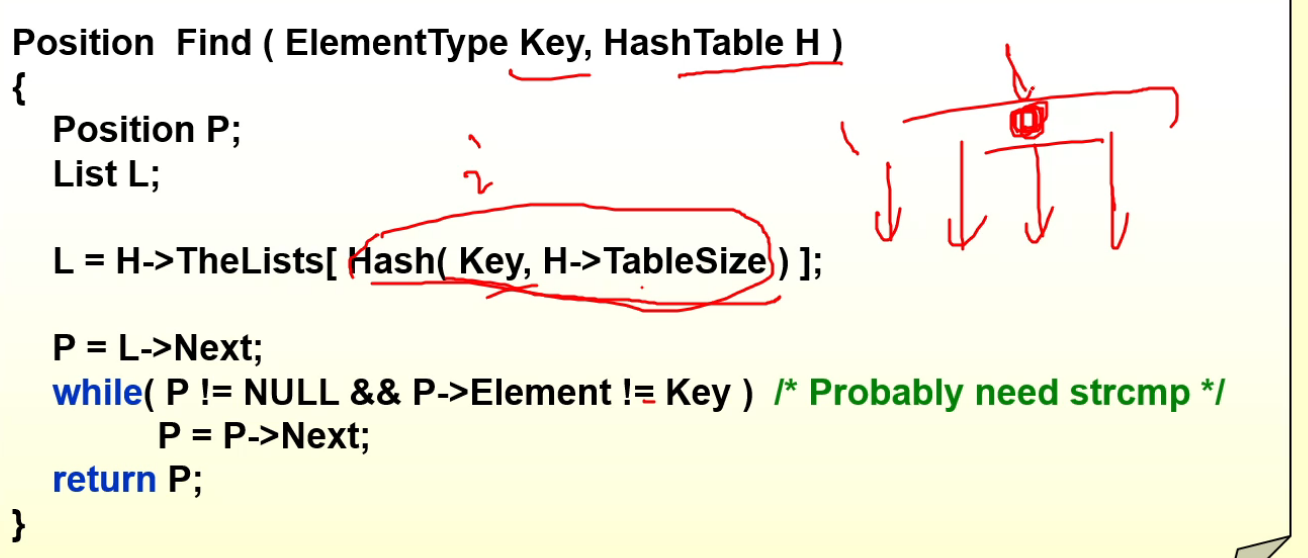
Find¶
- 通过算法算出哈希值，这就是链表所在地；
- 在单向链表里寻找；
Insert¶
- 首先Find，看看元素在不在里面，如果在里面就不需要插入了；
- 先申请空间，然后开始插入；
- 先算出哈希值，然后接入（链表头插入）；
- 先算出哈希值，然后接入（链表头插入）；
1 HASHING（12.20）¶
1.4 Open Addressing¶
基本思路¶
不断增加偏移量，看有没有冲突；
1 线性探测¶
-
平均成功查找次数（枚举法即可）
-
平均不成功查找次数：根据哈希函数不成功查找的字符串分成若干种类型，全部加起来，除以类的总个数；
2 Quadratic Probing¶
如果加的超过范围了就求余，二次查找避免了拥挤，但是他不一定能够找到空位；
一些其他方法¶
Find Insert and Delete¶
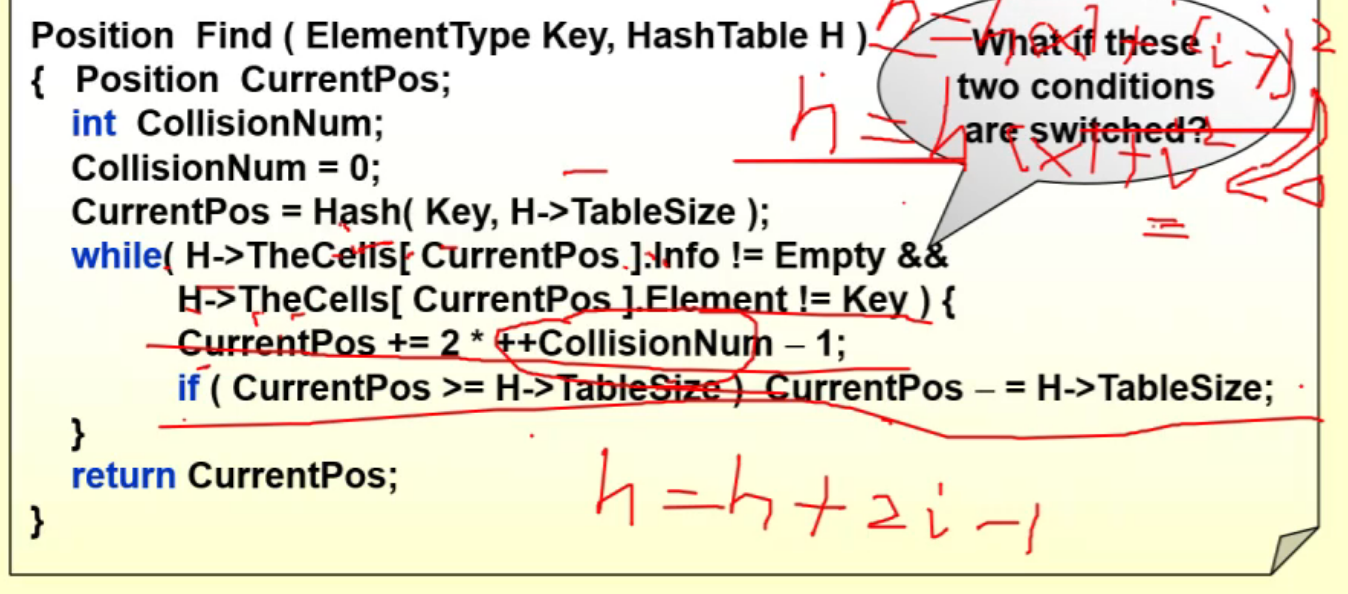
3 Double Hashing¶
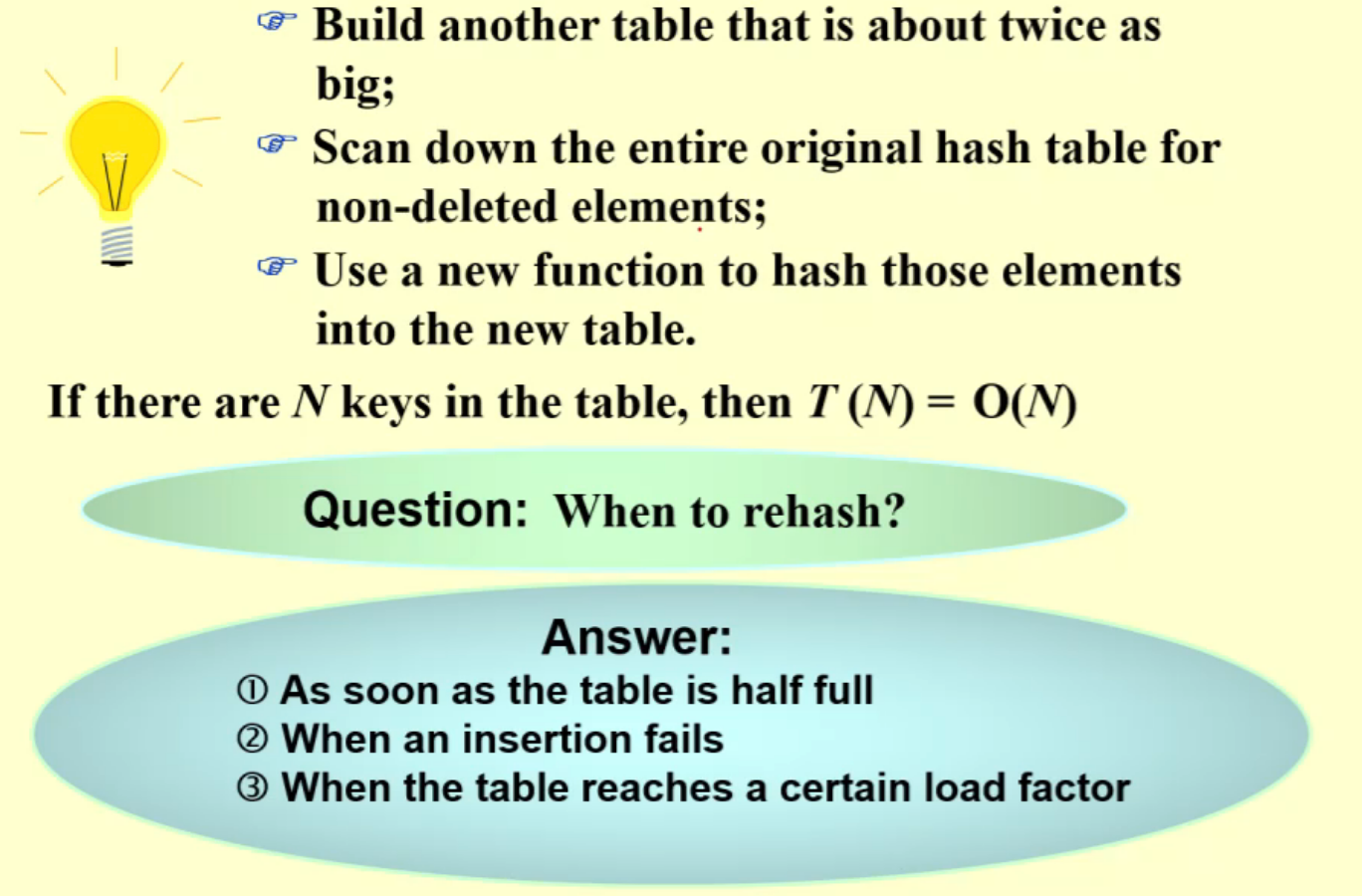
4 Rehashing¶
本文总阅读量次