lec8
约 609 个字 16 张图片 预计阅读时间 2 分钟
1. 一些定义¶
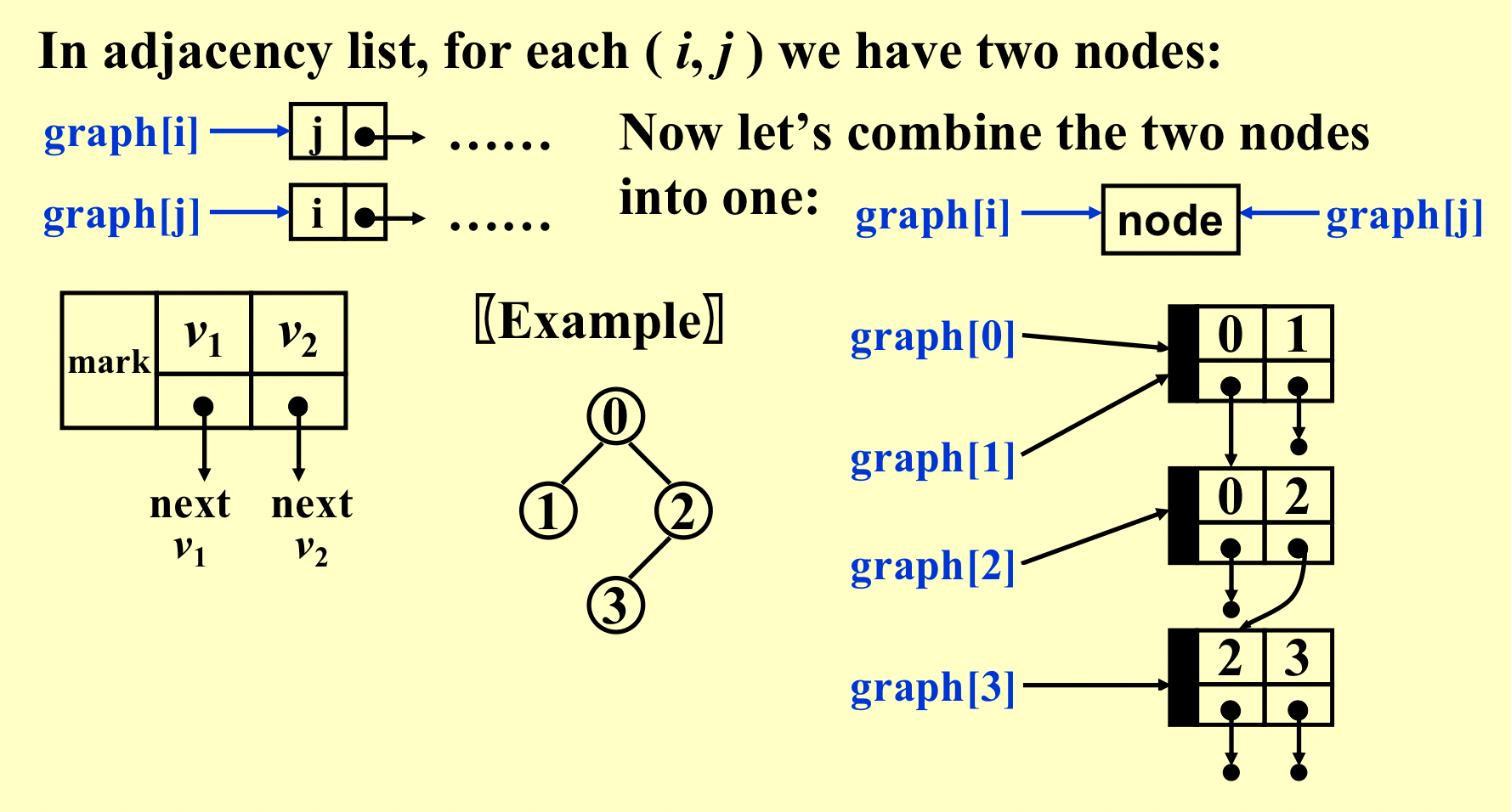
Adjacency Lists(邻接表)¶
指出去的表;
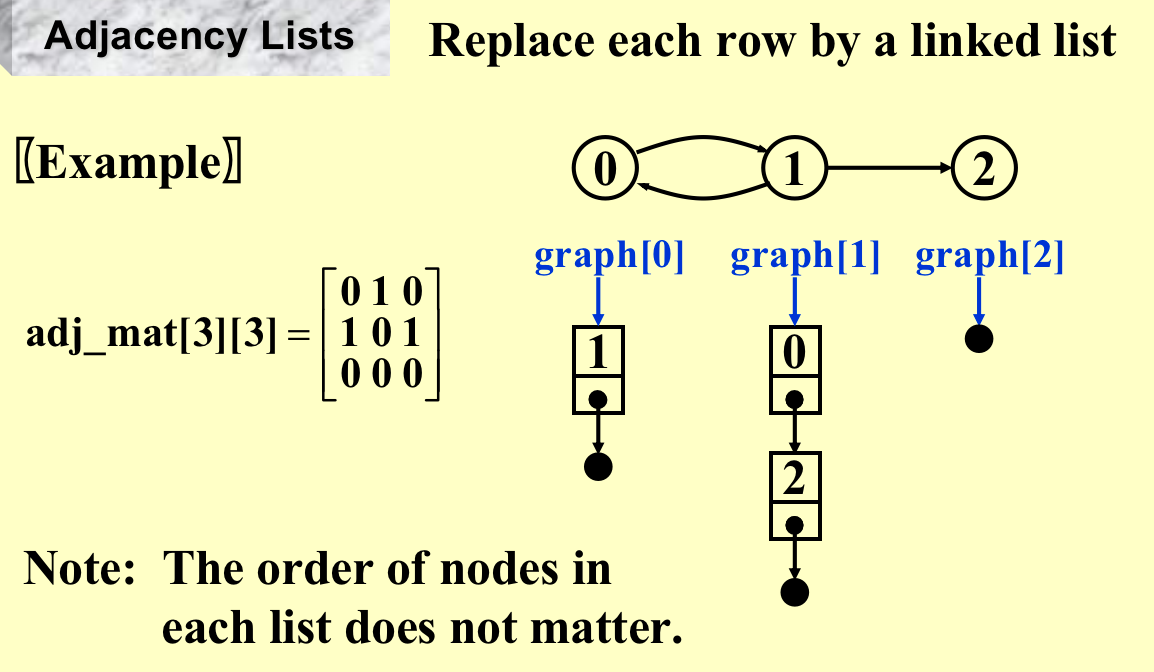
逆邻接表¶
指进来的表;
合并成十字链表¶
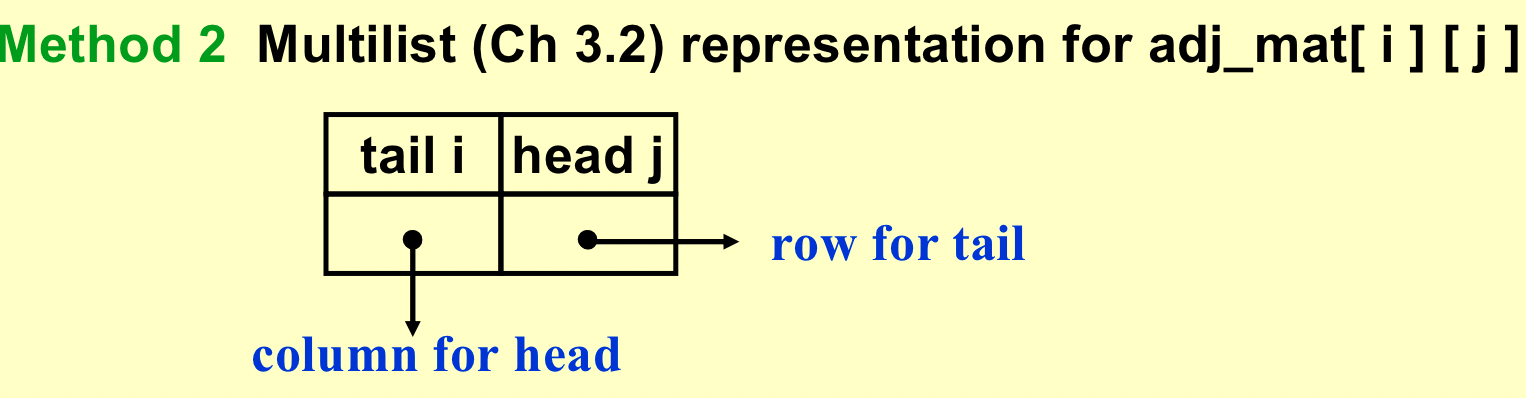
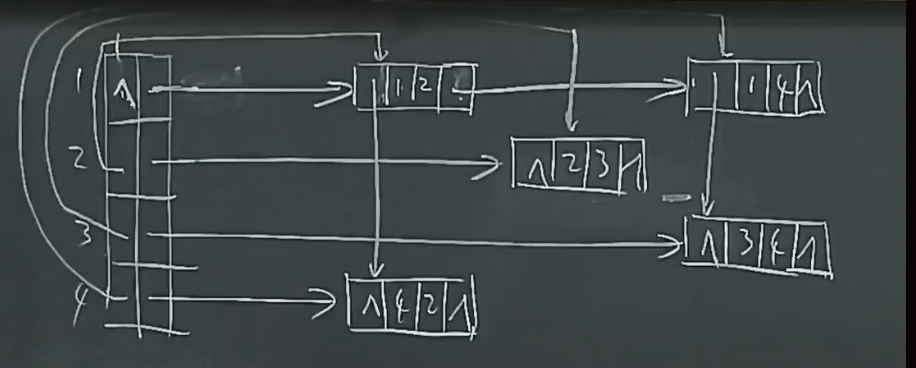
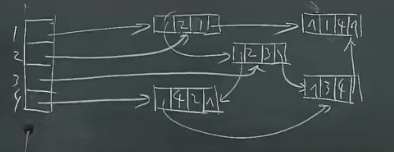
Adjacency Multilists(多重链表)¶
对于无向图:
- 若使用邻接矩阵,五条边要有十个结点;
- 类似上方的无向链表,构建多重链表;
- 多重链表左右位置互换都没有关系;
2. Topological Sort(拓扑排序¶
一些定义¶
- DAG:有向无环图;
- AOV:用点来表示对象;

- AOV特征:传递性但不是对称的;


- 拓扑排序:一个一维序列,满足二维的表的关系即可;

找拓扑排序¶
方法一¶
- 拓扑排序第一个点入度为0;
- 对indegree数组进行查找,找到入度为0的点,若没有,则说明有回环,error;
- 找到后,进行相应的输出;
- 每次删除一个点后,把对应的出度的边也删除,把这个边的入度点的入度减1;

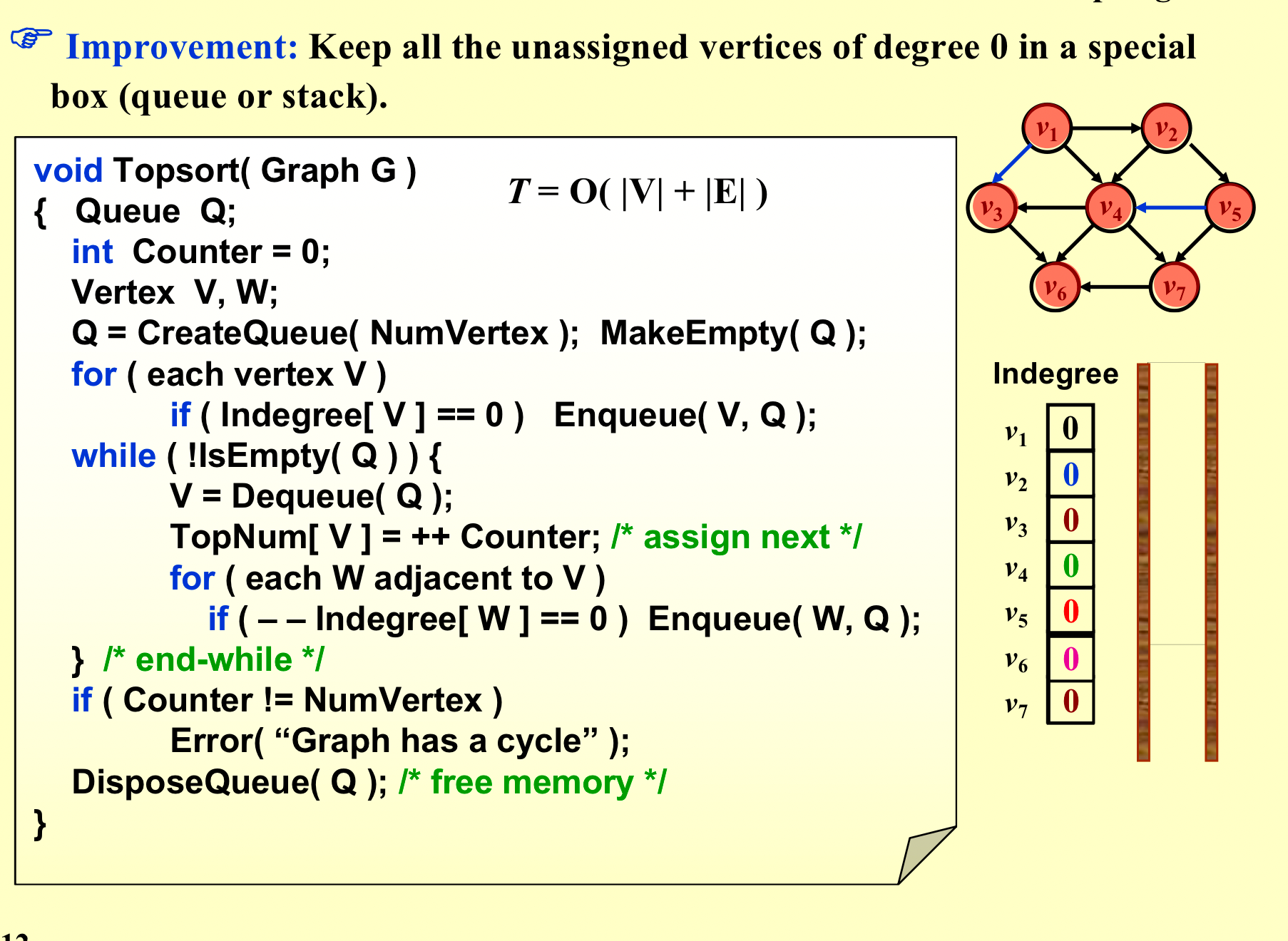
方法二¶
- 创造一个队列;
- 找出所有入度为0的点,压入队列;
- while(!Isempty(Q))
- 一个元素出队列,并放入输出列表;
- 对于所有和此元素相连的元素,把他们的入度都减一,并判断是否在修改过后,入度为0;
- 如果输出列表还没满就出来了,说明有环,error;
3. Shotest Path Algorithm¶
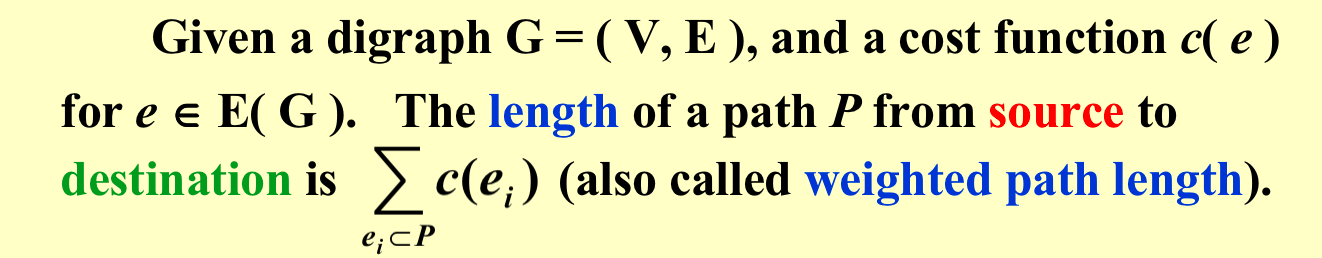
3.1 Single-Source Shortest-Path Problem¶
Given as input a weighted graph, G = ( V, E ), and a distinguished vertex, s, find the shortest weighted path from s to every other vertex in G.
3.1.1 Unweighted Shortest Paths¶
- 距离为0列出所有,距离为1列出所有.......(宽度遍历);
- 实现思路:
- Table[ i ].Dist:最短路径的长度;
- Table[ i ].Known:是否已经算过,比如算2的时候,1就不用再算了;
- Table[ i ].Path:记住上一个人;
- 实现代码(已知一个点的路径信息,修正附近点的路径信息);


3.1.2 Dijkstra’s Algorithm (for weighted shortest paths)¶
- 在unkown的点中,dist值最小的点就是最短路径;
- 找最小值可以用堆来提高效率;

3.1.3 Graphs with Negative Edge Costs¶
- 原来是标记为known后不去碰它,但是有负数之后还是需要遍历known;没有known和unkown之分;
- 如果队列中已经有自己了,就不用再入队了;
- 因为每循环一次少一个点,当有更新的时候,就会入队,队列为空就结束;

4. Acyclic Graphs¶
-
AOE——边代表对象(任务),边的权重代表时间,点代表依赖关系;
-
关键路径查找;
本文总阅读量次