lec9
约 245 个字 15 张图片 预计阅读时间 1 分钟
1. Acyclic Graphs¶
- CPM(Critical Path Method)
- 边之间有先后关系;
- 边有权重;
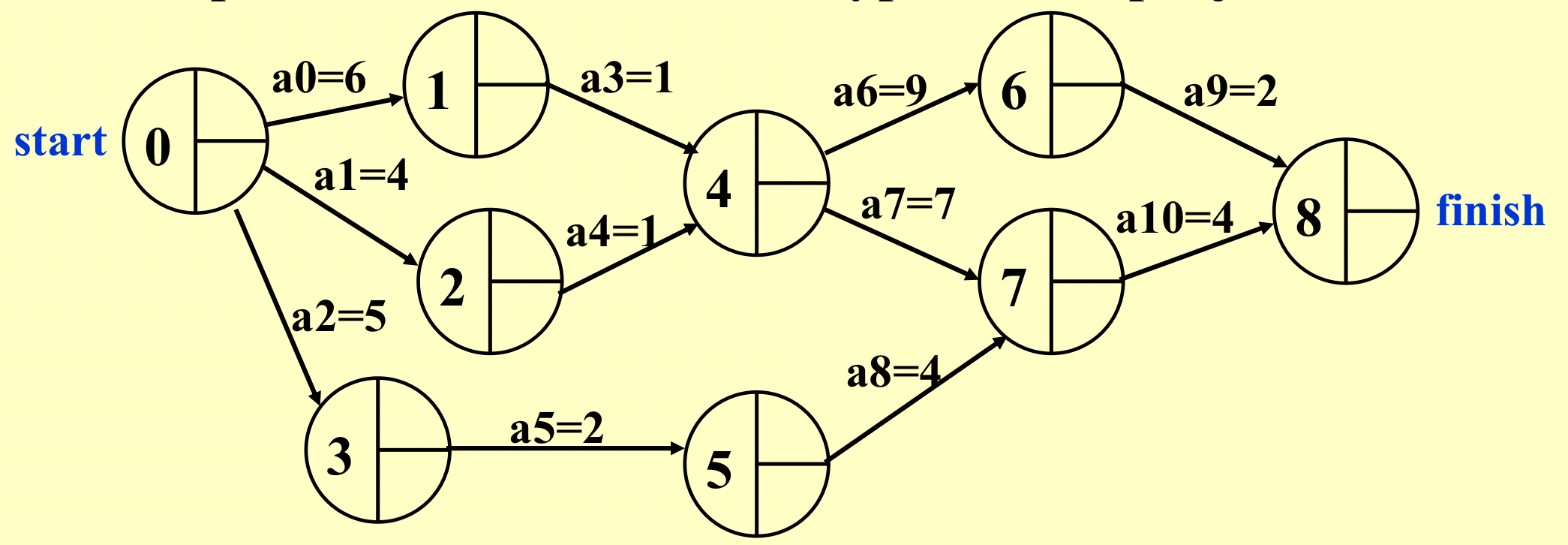
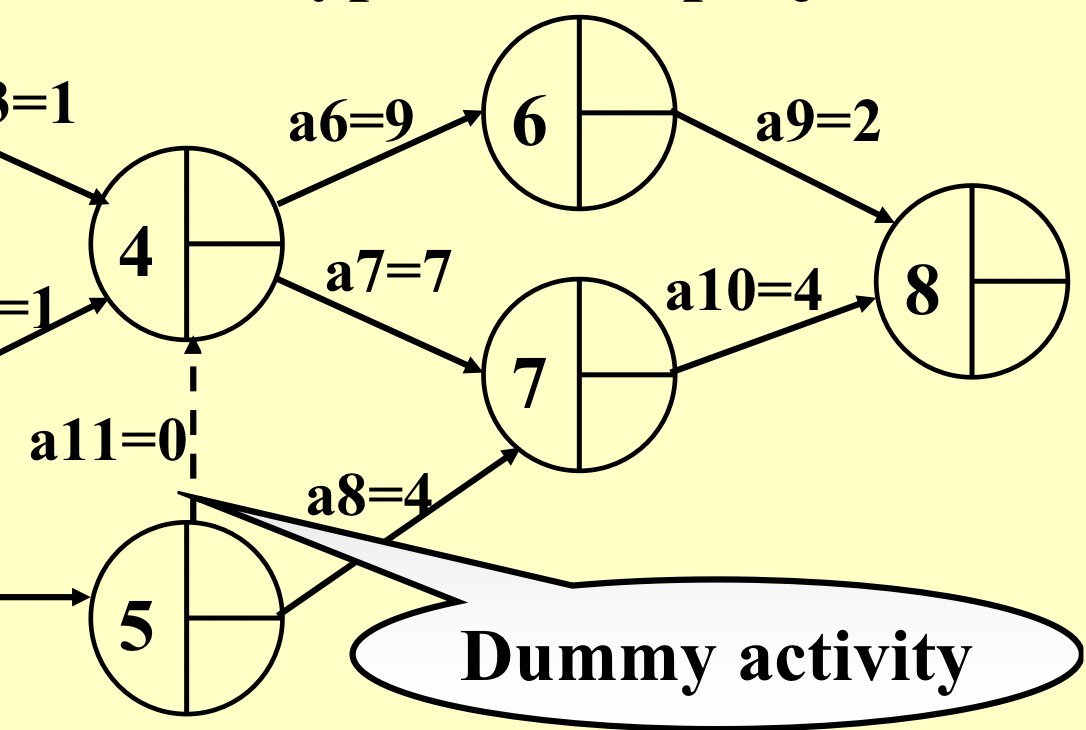
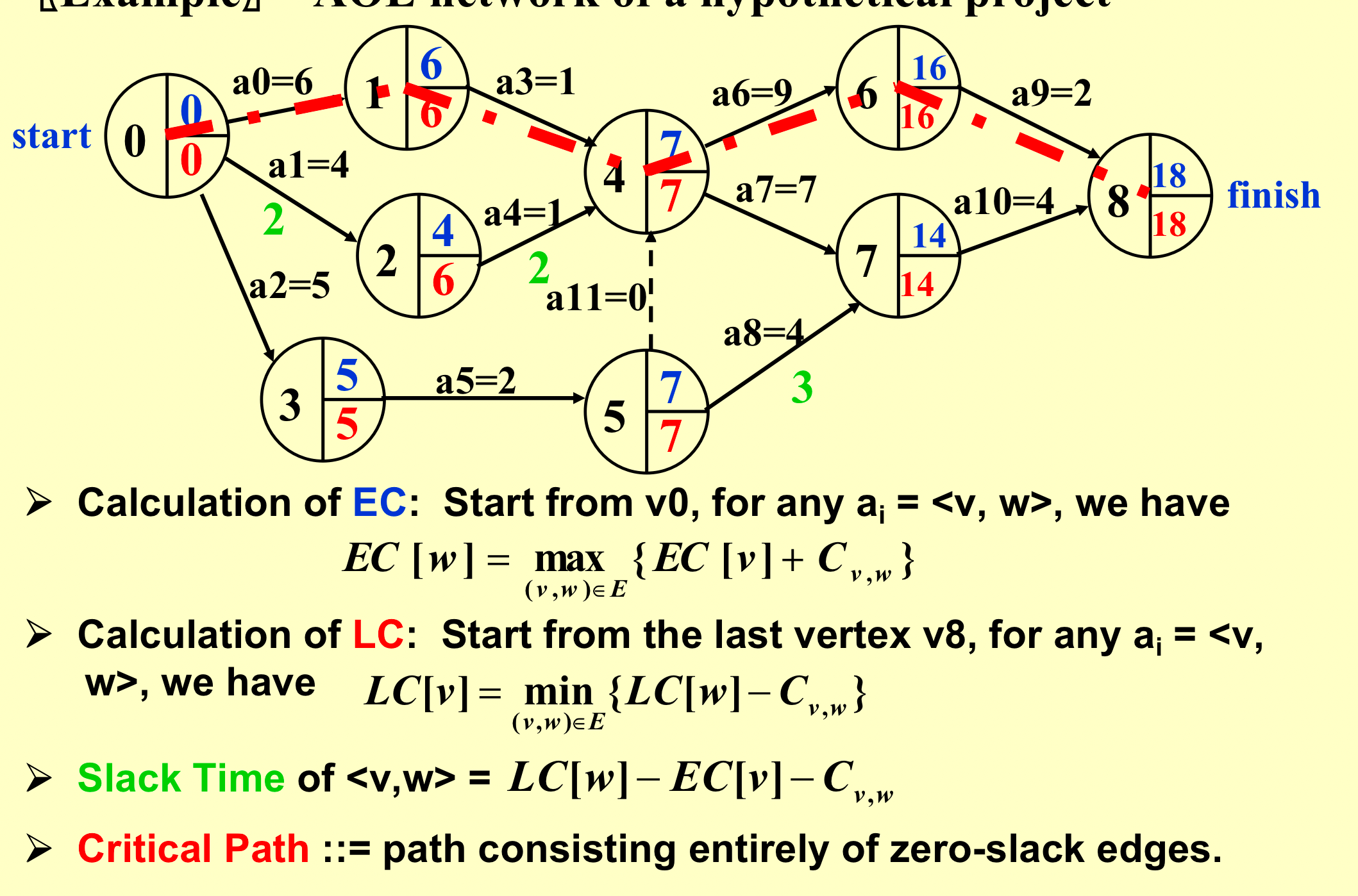
- 解决方案:
- 算出每个结点最早结束的时间,左边到自己的最大值;
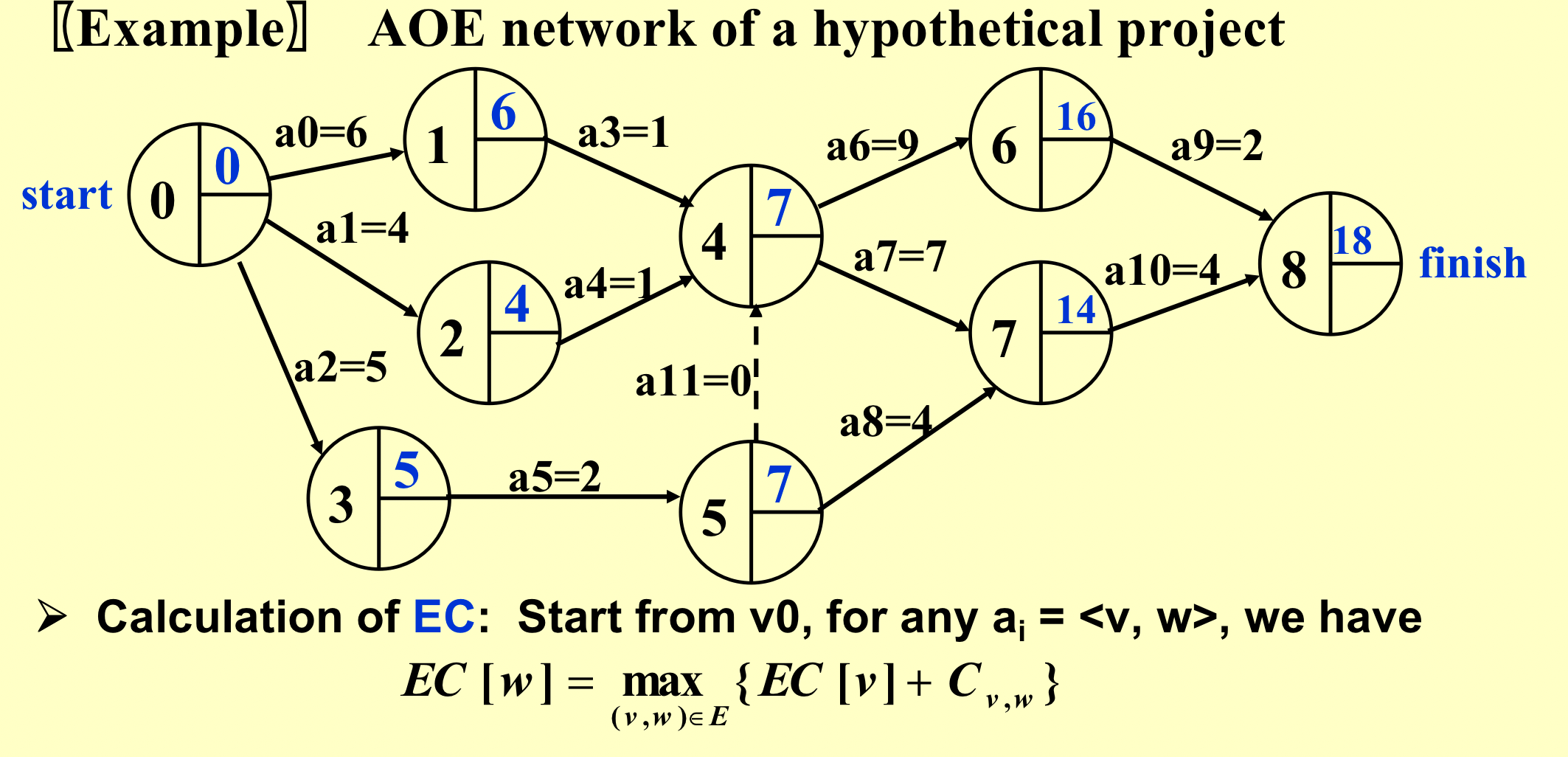
- 算出每个结点的可以的最晚时间。右边到自己的最小值;
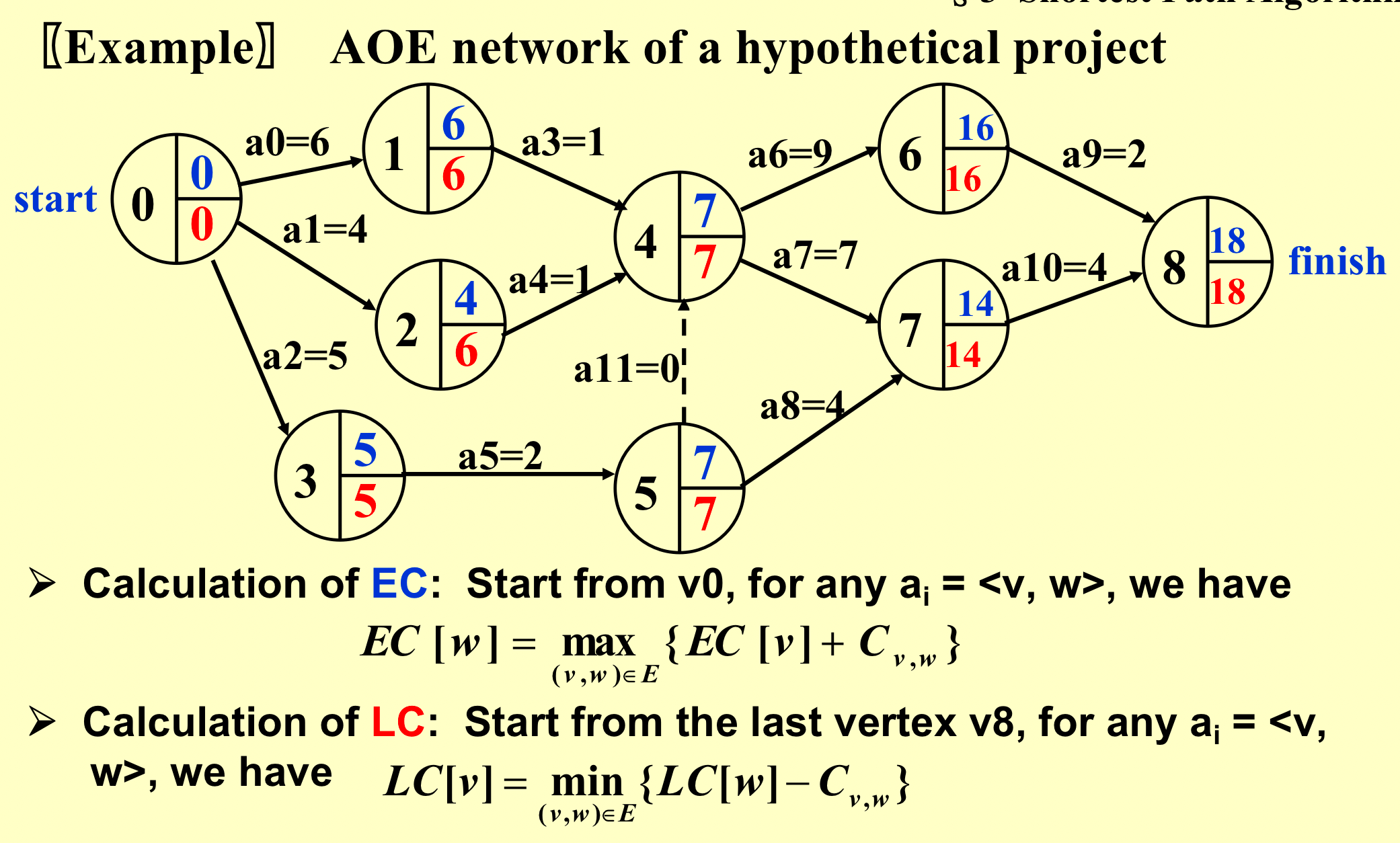
- 算出拖延时间;
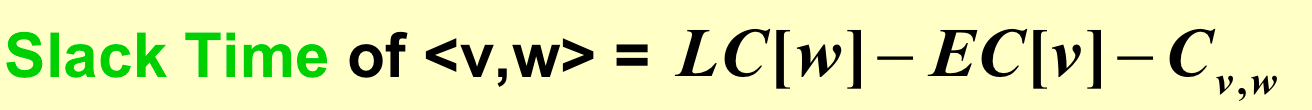
- 所有不能拖延的点连起来就是关键路径;
2. All-Pairs Shortest Path Problem¶


3. Network Flow Problems¶
-
求出从起点到终点最大流量是多少;
-
解决方法一:
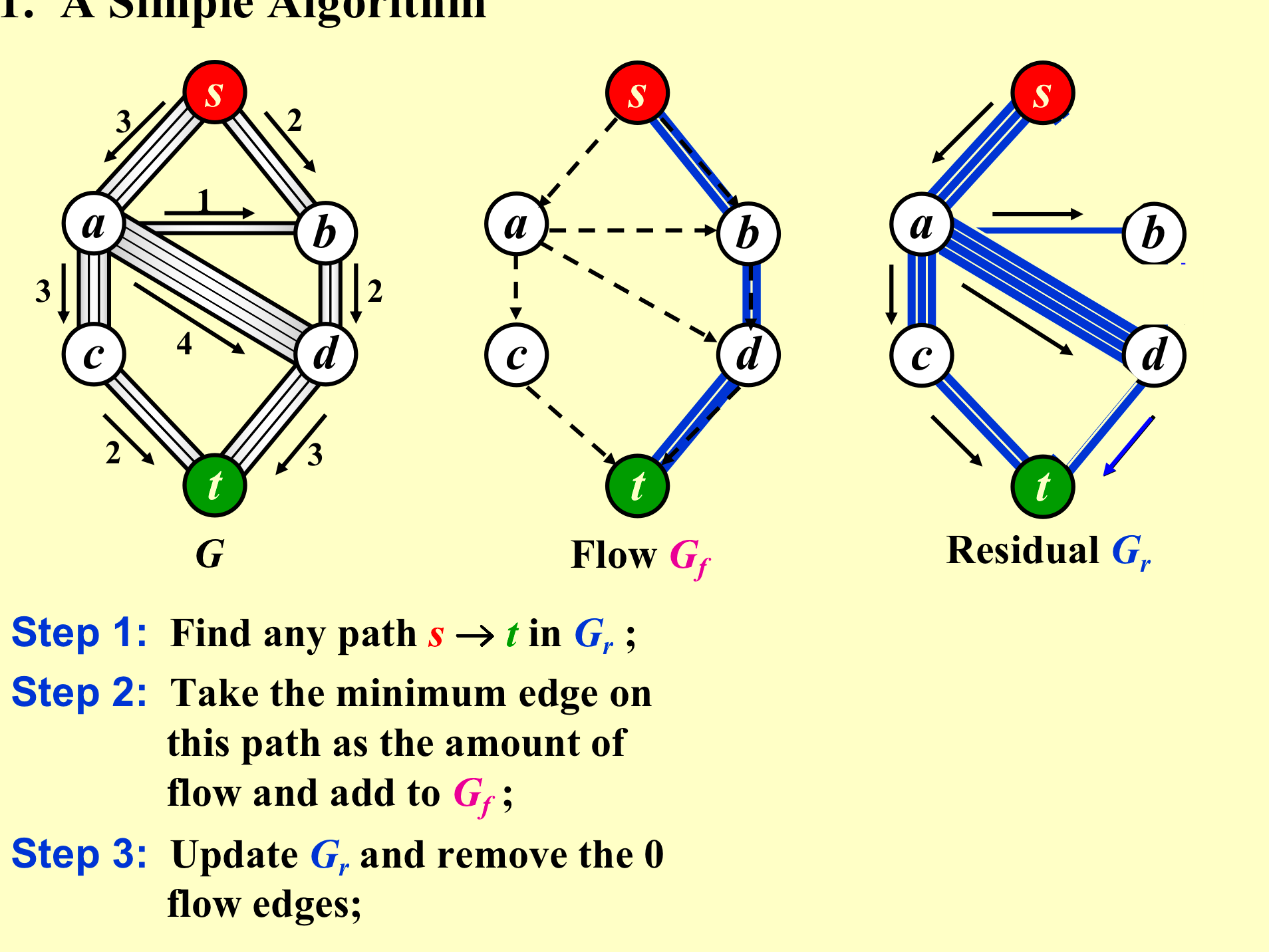
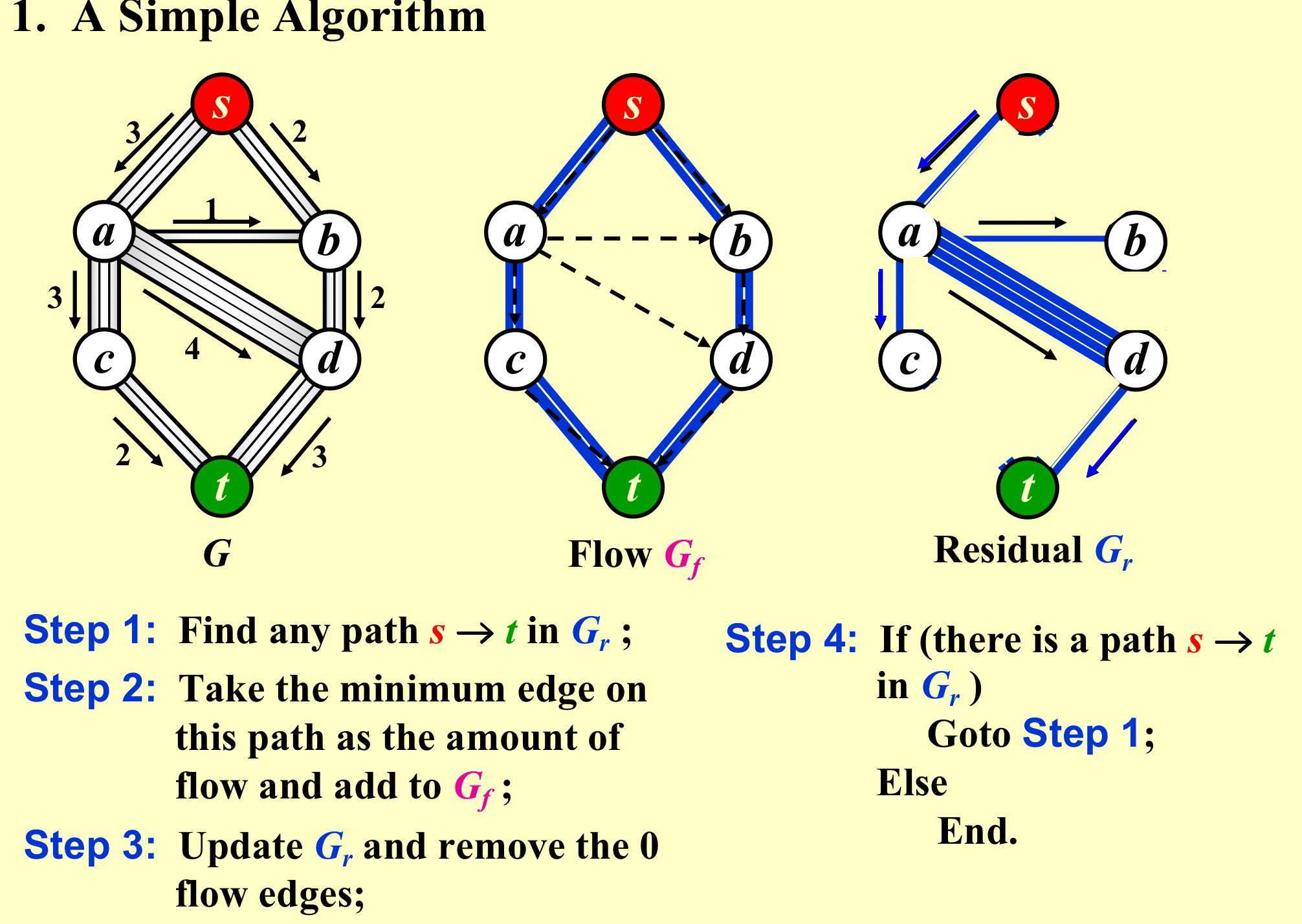
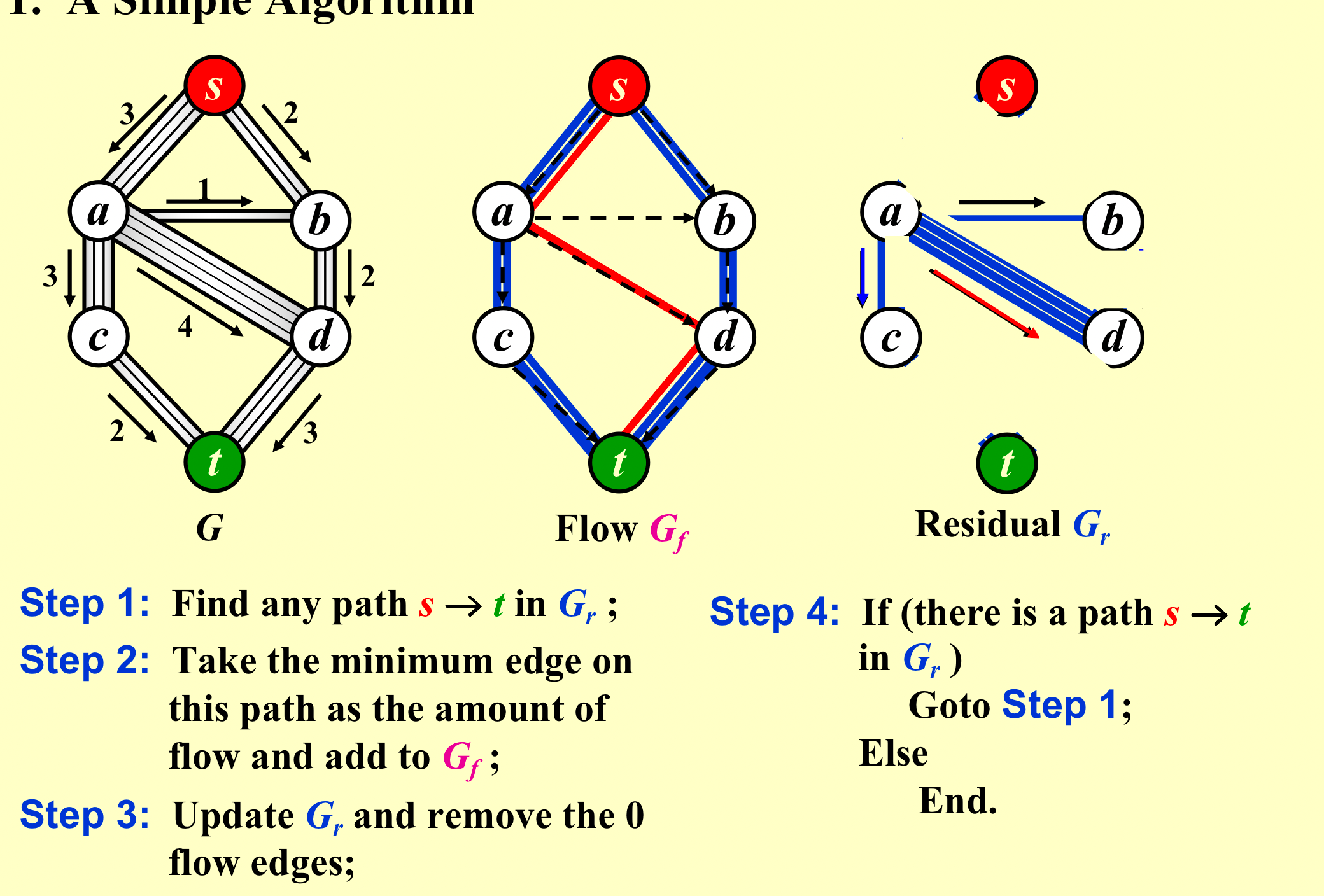
-
这个方法不一定能找到最佳路径,挑错了就找不到最优解了;
-
解决方法二(allow the algorithm to undo its decisions )
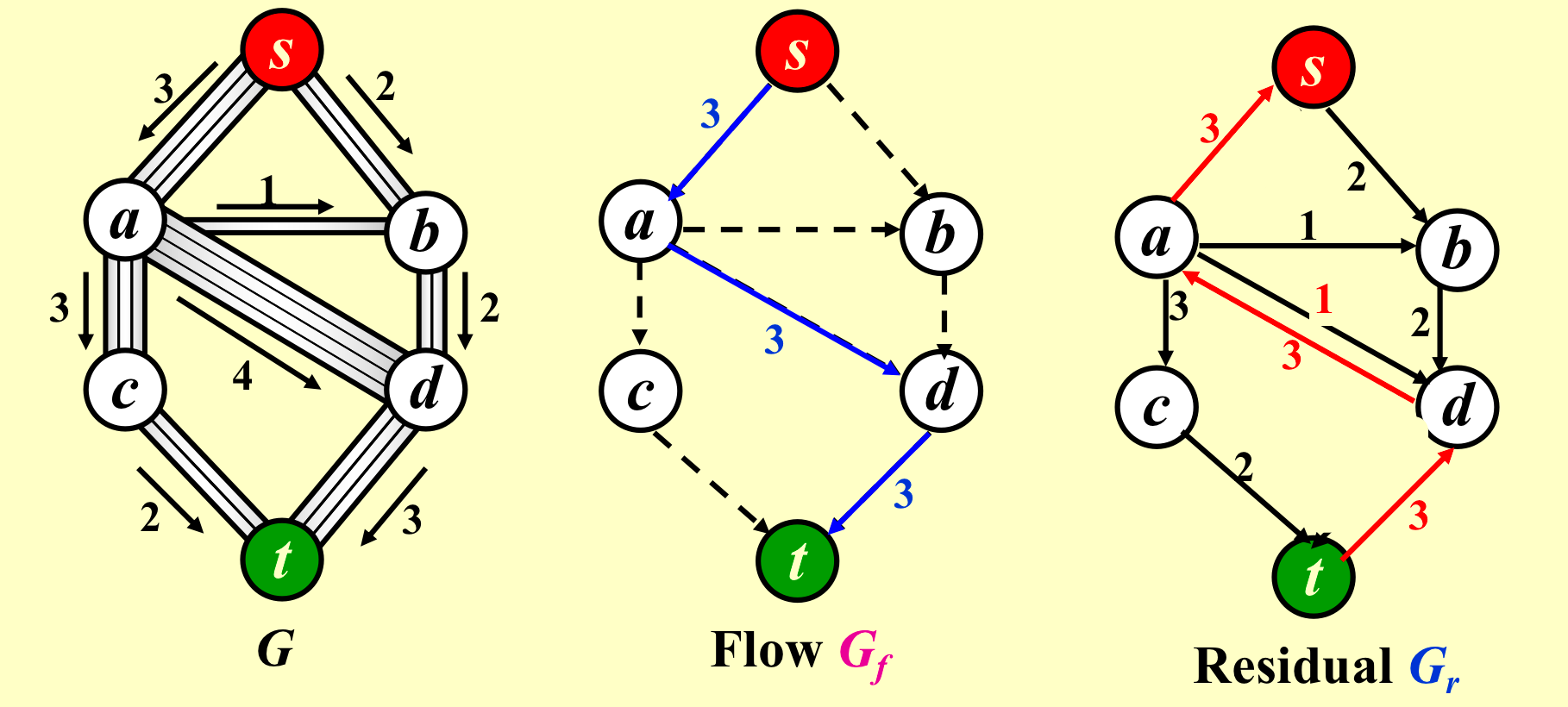
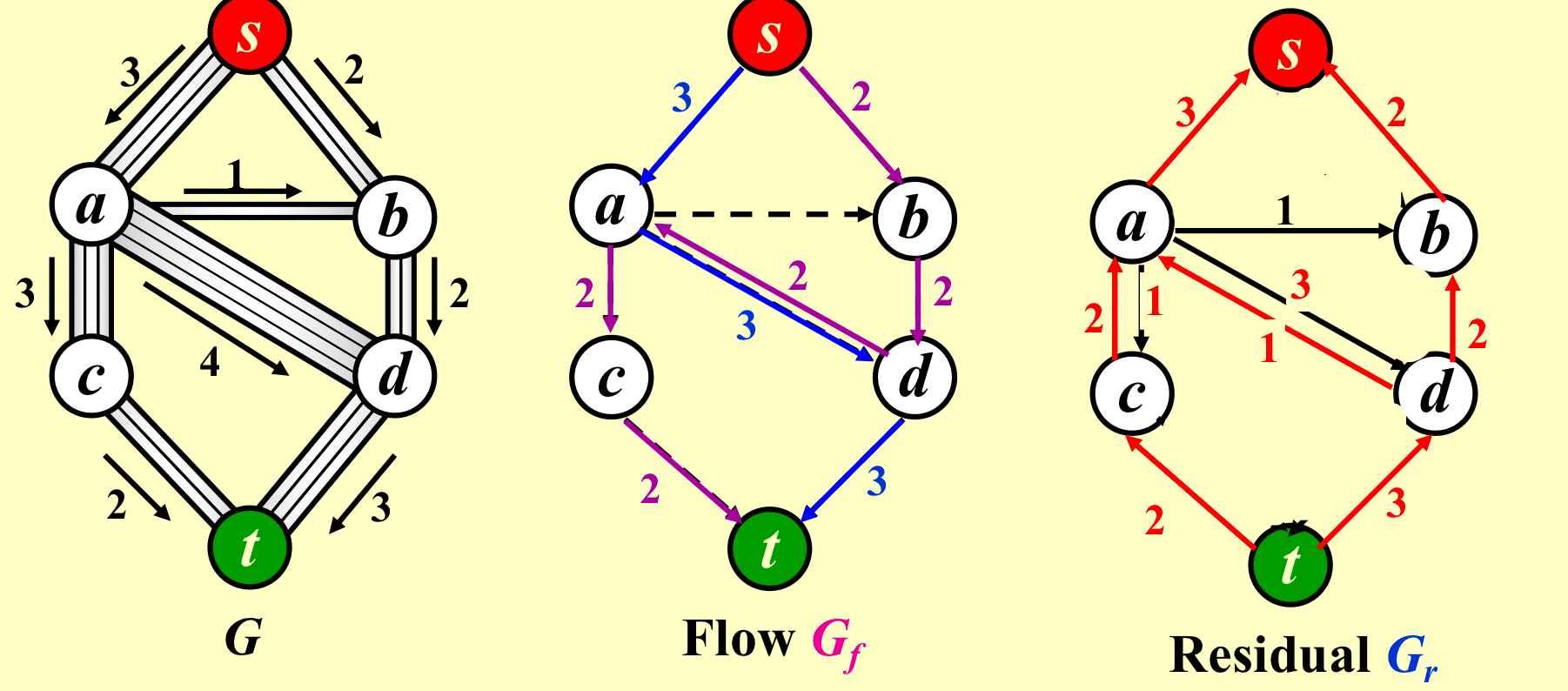
- 老师这个问题一笔带过了……
4. Minimum Spanning Tree¶
- n个结点,n-1条边,是连通的生成树;
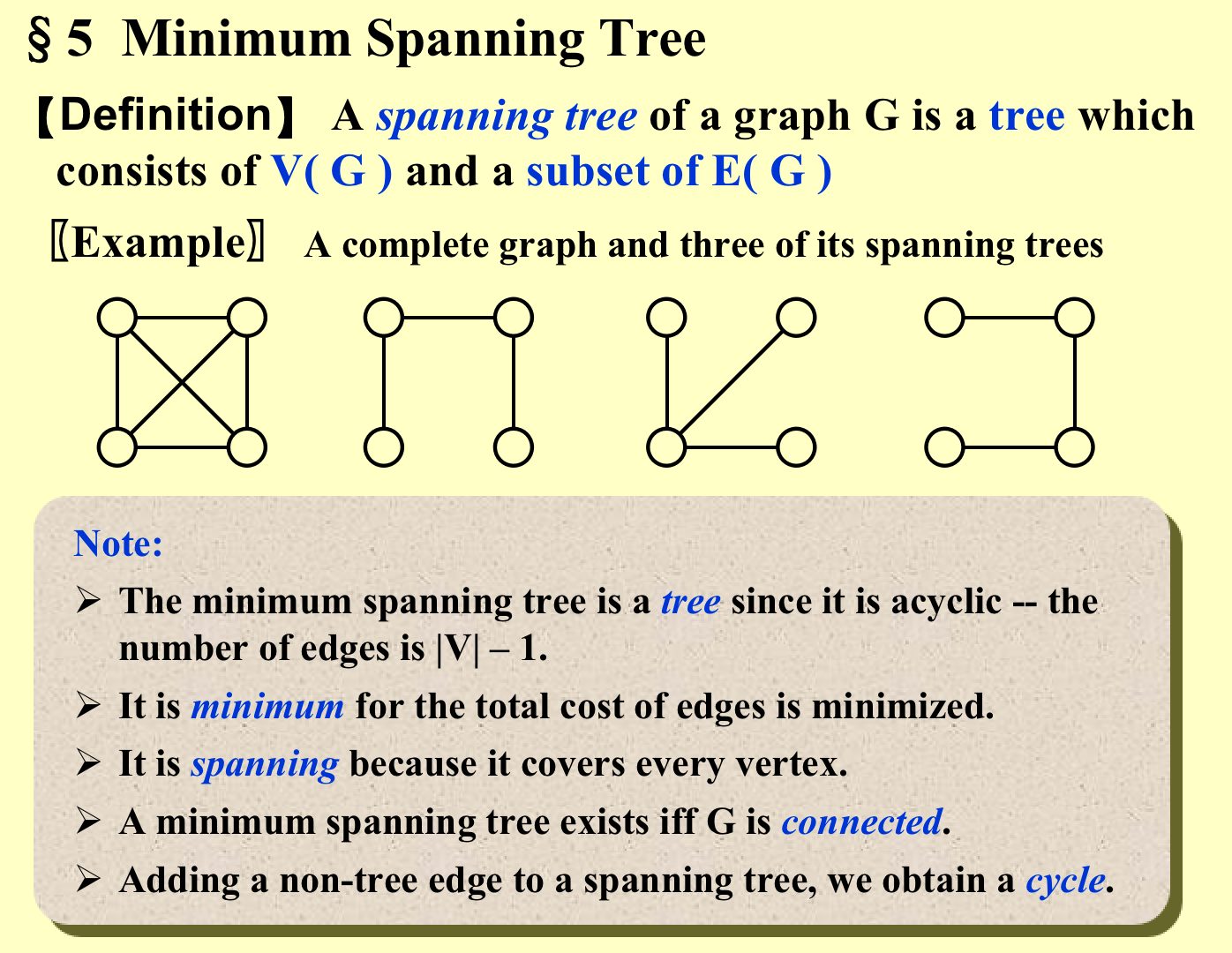
- Kruskal’s Algorithm(以边为核心)

-
判断是否有环可以使用等价类,利用Unionfind,连一起就是同一个等价类;
-
Prim’s Algorithm(以点为核心)
- 找出跟局部生成树连接最小边并一直保持是树;
本文总阅读量次